スタクラ情報局

正弦定理とその証明

数学 I 「図形と計量」で学習する正弦定理。

当たり前のように使っているかもしれませんが、そもそも正弦定理がなぜ成り立つのか、気にしたことはありますか？

学校の定期試験などでも、定理の証明が求められるかもしれません。

そこで今回は、正弦定理の証明を説明していきます！

正弦定理とは

まずは正弦定理がどういうものか、復習しましょう。

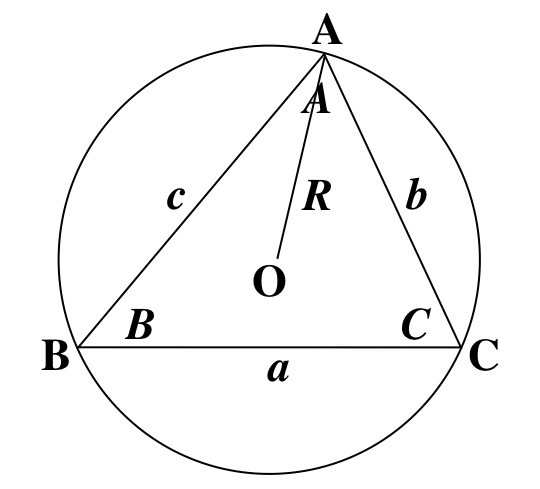
△ABC の各辺の長さや角度、そして外接円の半径に上のような名称をつけます。

このとき、次が成り立ちます（正弦定理）：

正弦定理の証明

ではいよいよ、正弦定理の証明をしていきます。

鋭角三角形なのか鈍角三角形なのかで、図形の位置関係が変わってくるので注意が必要です。

鋭角三角形の場合

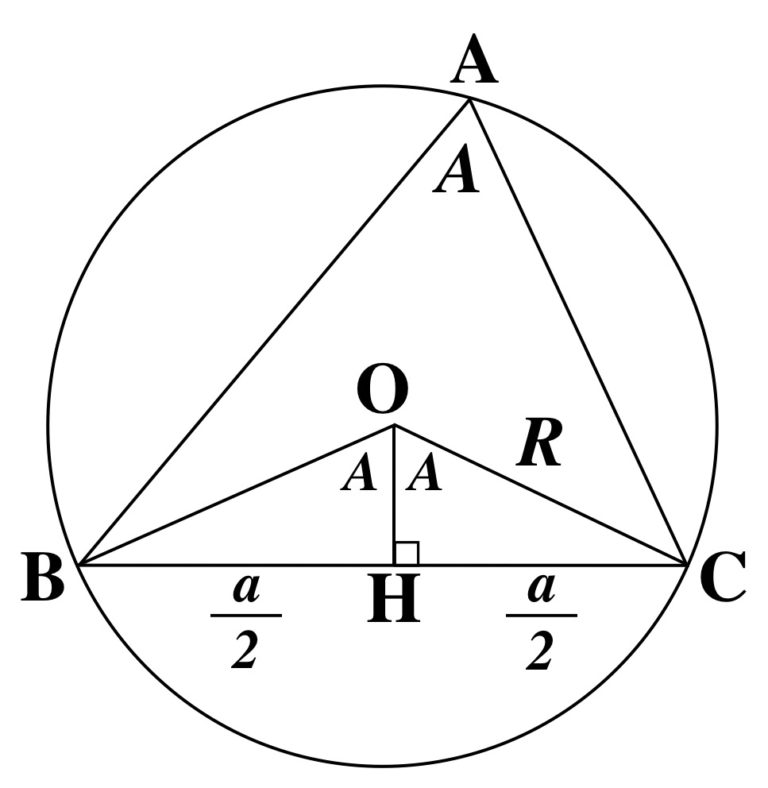
△ABC が鋭角三角形のとき、各点の位置関係は上図のようになります。

鋭角三角形の場合は、特に ∠A について示せば十分です。

上図のように、外接円の中心 O から辺 BC に下ろした垂線の足を H としましょう。

円周角の定理より ∠BOC = 2A となり、△BOH ≡ △COH ですので（※） ∠BOH = ∠COH = A および BH = CH =  がしたがいます。

ここで △COH に着目しましょう。これは ∠OHC = 90º の直角三角形です。

したがって、正弦の定義から CH = OC sinA となるので、

となり、A と a について部分的に正弦定理が成り立つことがわかりました。

B と b 、C と c についても同様のことがいえるため、鋭角三角形では正弦定理が成り立つことが示せました。

※ OB = OC (円の半径), OH = OH (共通) および ∠OHB = ∠OHC = 90º が成り立ち、直角三角形で斜辺と他の 1 辺がそれぞれ等しいので、△BOH と △COH は合同となります。

直角三角形の場合

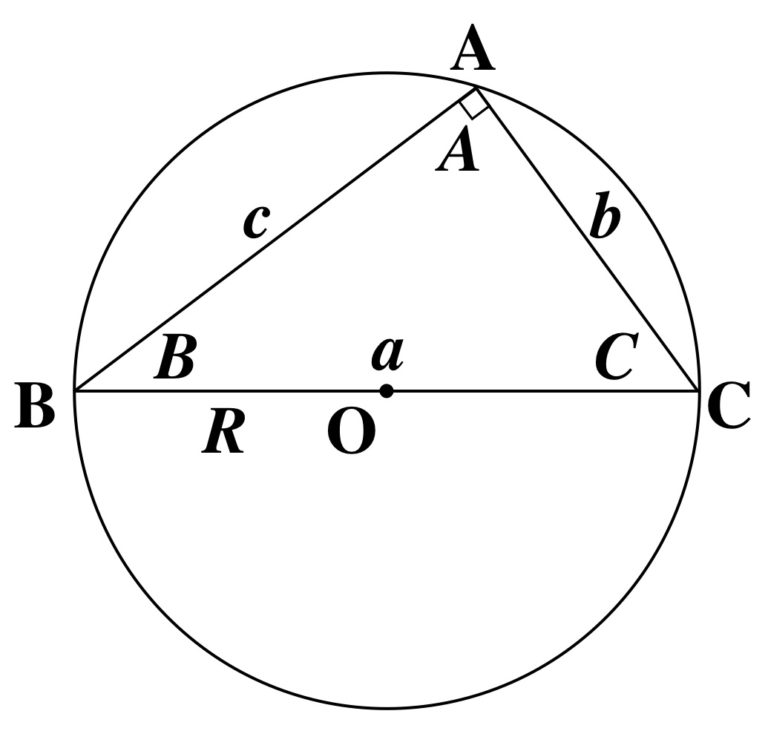
∠A が直角であったとしましょう。

このときの位置関係は上図のようになります。特に辺 BC は円の直径となっていますね。

まず A = 90º より sinA = 1 であり、a = BC = 2R であるため、 は成り立っています。

∠B について考えると、A = 90º より  ですので、 が成り立っています。

同様にして もいえるため、直角三角形においても正弦定理が成り立つことが示されました。

鈍角三角形の場合

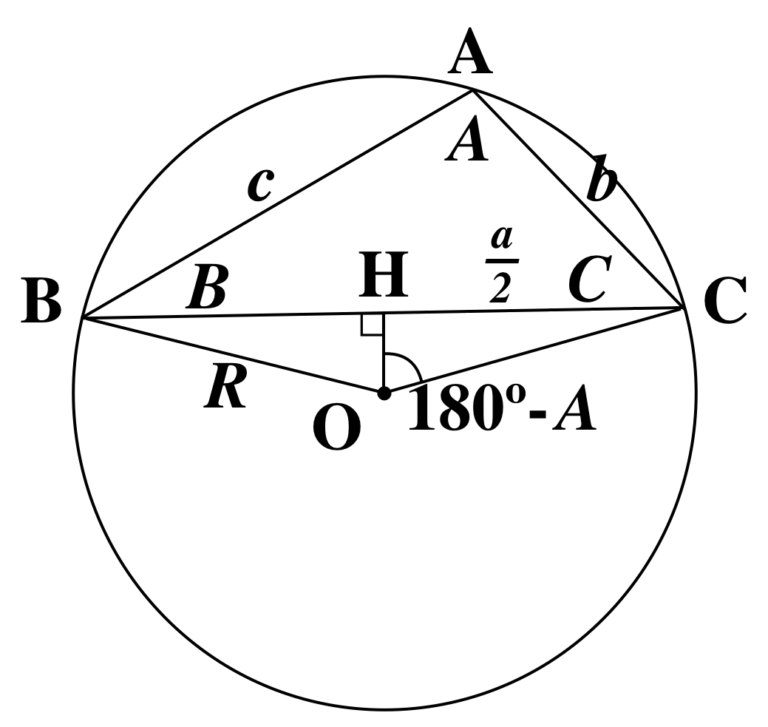
∠A を鈍角としましょう。

鋭角の場合と異なり、点 A と点 B, C は別個に証明する必要があります。

まずは A, a について証明していきます。

外接円の中心 O から辺 BC に垂線 OH を下ろします。

円周角の定理より、大きい方の ∠BOC は 2A となります。

よって小さい方の ∠BOC は 360º - 2A です。

△BOH ≡ △COH ですので、∠BOH = ∠COH =  なります。

sin∠COH = sin(180º - A) = sinA なので、

したがって となり、A, a について部分的に正弦定理が成り立つことがわかりました。

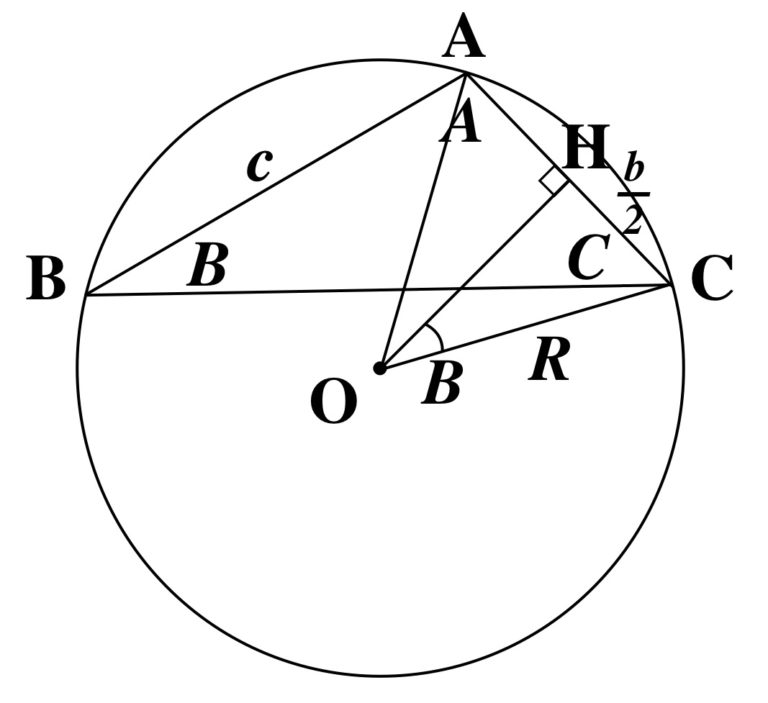
鈍角でない角度についても証明する必要があるので、B, b について証明をしておきます。

外接円の中心 O から辺 AC に垂線 OH を下ろします。

円周角の定理より ∠AOC = 2B となります。

△AOH ≡ △COH が成り立つため、∠AOH = ∠COH = B および AH = CH =  となります。

ここで △COH に着目すると、 であるため となり、これより  がしたがいます。

同様に が成り立つことも証明できます。

まとめ

正弦定理の紹介をし、その証明を

・鋭角三角形の場合
・直角三角形の場合
・鈍角三角形の場合

に分けて行いました。

もう一度、正弦定理の公式の形をみておきましょう：

正弦定理は「図形と計量」の分野で習う重要定理ですが、これが成り立つ証明を理解している人は少ないのではないでしょうか？

鋭角三角形などの単純なケースで証明を要求されることはあるので、定理の形を覚えたら証明も勉強してみましょう。

正弦定理と並んで重要な「余弦定理」の紹介と証明は、こちらの記事で扱っています：

正弦定理・余弦定理を用いた三角形の決定問題などは、こちらの記事で扱っています：