スタクラ情報局

余弦定理の公式

この記事では、余弦定理の公式やその証明を扱っていきます。

「図形と計量」に登場する重要な定理。

証明も含め、ここで理解しちゃいましょう！

※正弦定理の説明や証明は、別のページで扱っています。

文字の定義

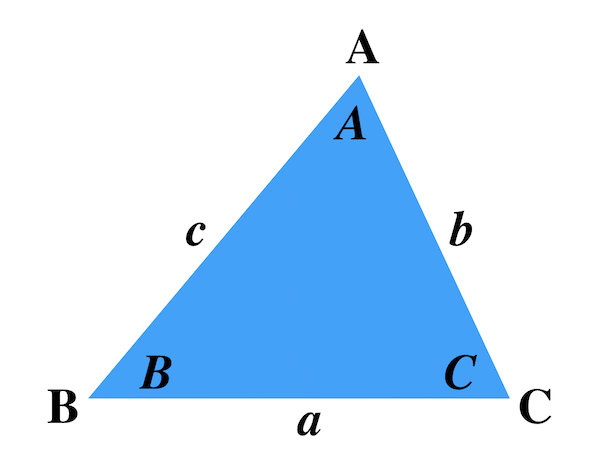
三角比の分野には、角度・辺の長さの表し方の慣習があります。

△ABC において AB = c, BC = a, CA = b, ∠ABC = B, ∠BCA = C, ∠CAB = A と表記します。

問題集・教科書問わず共通した表記で、余弦定理や正弦定理の公式にも頻繁に登場します。

知らなかった人はこの場で頭に入れてしまいましょう！

余弦定理とは

余弦定理は、三角形の辺の長さと角度について成り立つ定理で、公式の具体形は次の通りです：

公式に余弦 (cos) が登場しているので、余弦定理という名前になっています。

上の図も参照して、辺の長さや角度がどのように使われているか確認してみましょう。

前提：三平方の定理

次に説明する余弦定理の証明では、三平方の定理を用います。

＜三平方の定理＞

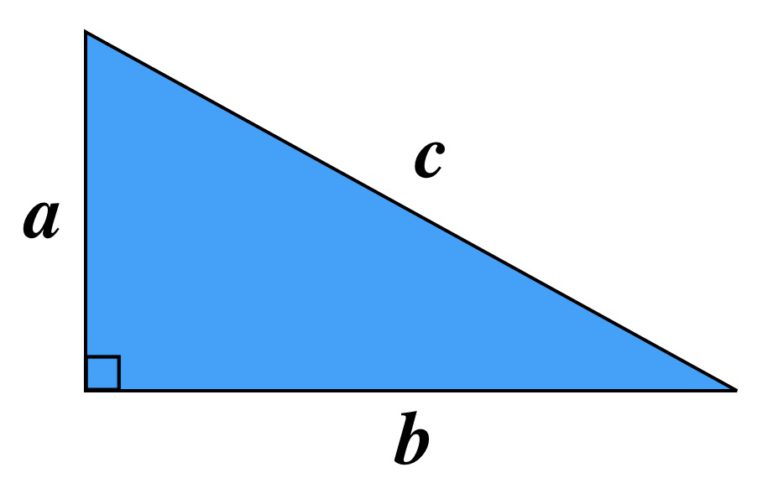
直角三角形の斜辺を c , その他の 2 辺を a, b とするとき、 が成り立つ。

中学校の幾何で学習する内容ですね。

三平方の定理の証明は多数存在しますが、ここでは省略します。

各自教科書を確認してください。

余弦定理の証明

では次に、余弦定理の証明をご紹介します。

証明自体が定期試験に出題される可能性もありますし、証明を知っておけば公式を忘れたときに思い出しやすくなります。

直角三角形などの特殊な三角形ではなく、一般的なケースを想定して証明しなければなりません。

一般性を確保するために、座標平面を利用します。

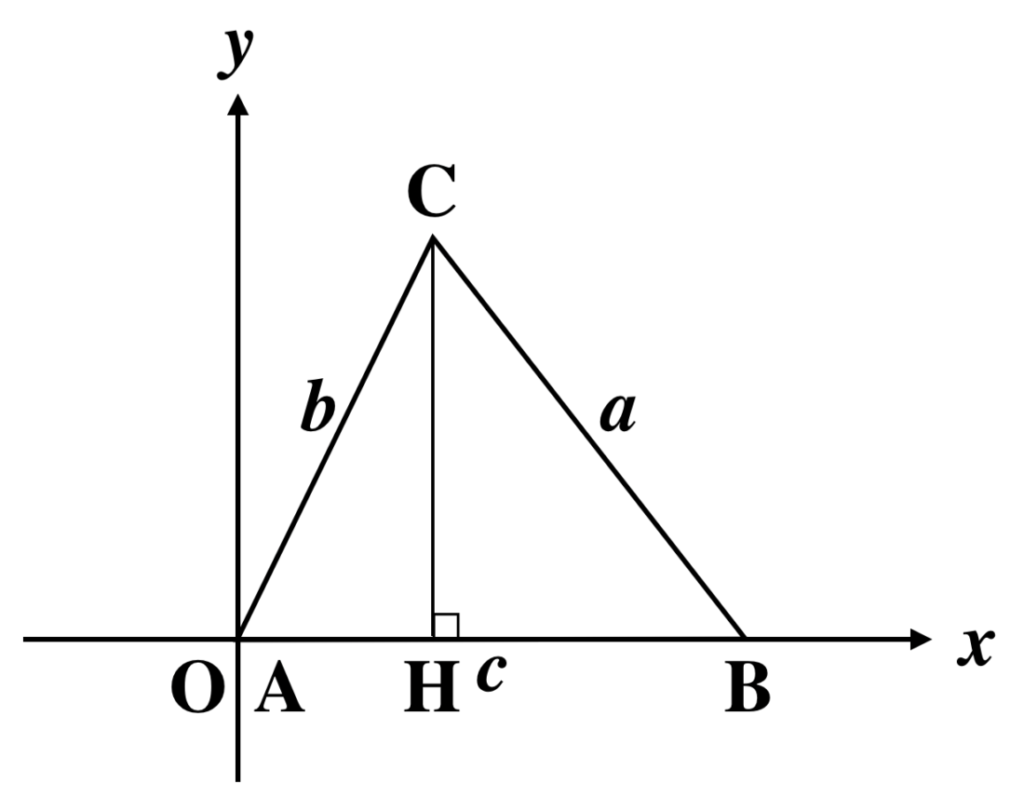
ここでは、 を示すことにします。（他の 2 つの式は、同じように証明可能）

△ABC を、
・点 A が原点と一致する
・辺 AB が x 軸の正の部分と重なる
ように配置します。

図では鋭角三角形を扱っていますが、後述するように鈍角三角形でも同様の議論ができます。

点 C から辺 AB に垂線 CH を下ろします。

さて、上図で余弦 (cos) の定義より OH = AH = b cosA が成り立ちます。

これより BH = AB - AH = c - b cosA です。

また正弦 (sin) の定義より CH = b sinA となります。

したがって、△BCH で三平方の定理より

ここで、三角比の基本公式  を用いると

と変形できるため、余弦定理の公式の一つ

が証明できました。

三角形の向きを変えて座標平面に再度配置すれば、他の 2 つの公式

も証明できます。

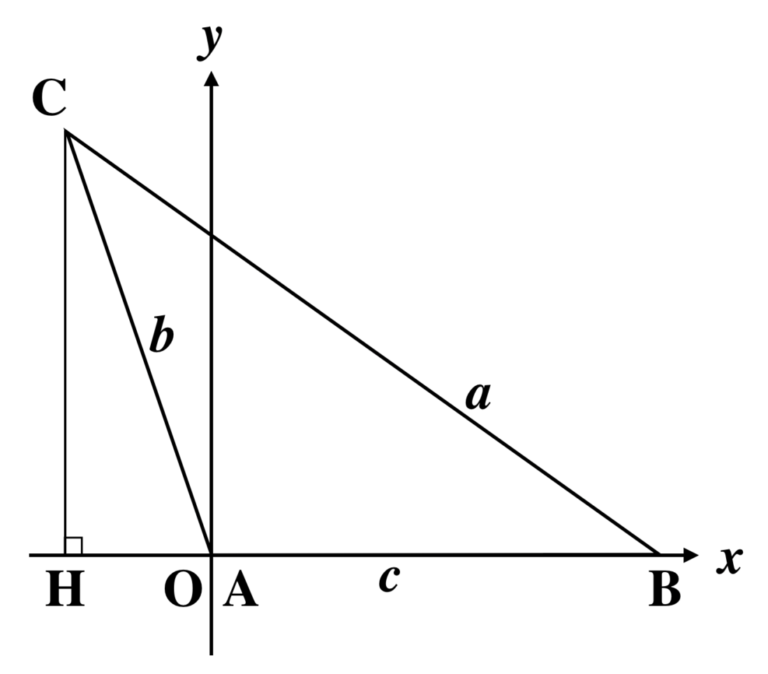
∠A が鈍角の場合、図形の位置関係は少々変わりますが、同様の議論ができることを確認しておきましょう。

先ほど同様に垂線の足を H とすると、ここでも点 H の座標は H(b cos A, 0) となります。（図形の位置関係の変化は、cos A の符号が担ってくれているわけです。）

三平方の定理より が成り立ちますが、結局計算式は  で変わりません。

△ABC が直角三角形のときでも三平方の定理の立式は同じになります。

まとめ

余弦定理の公式の紹介をし、その証明をしました。

もう一度公式の形をみておきましょう。

余弦定理は「図形と計量」の分野で習う重要定理ですが、これが成り立つ証明を理解している人は少ないのではないでしょうか？

鋭角三角形などの単純なケースで証明を要求されることはあるので、定理の形を覚えたら証明も勉強してみましょう。

余弦定理と並んで重要な「正弦定理」の紹介と証明は、こちらの記事で扱っています：

これらの定理を用いた三角形の決定問題は、こちら記事で扱っています：