数学Ⅰ 正弦定理 余弦定理

数学 I 「図形と計量」では、三角比を学習します。

今回は、そこで登場する２大定理である

• 正弦定理
• 余弦定理

の内容と、代表的な使い方を説明していきます。

文字の定義

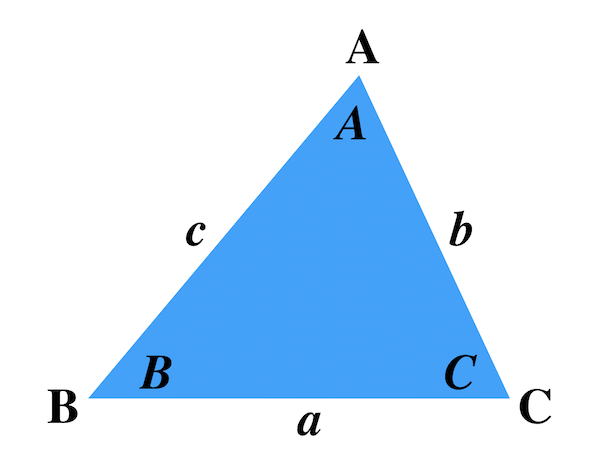
△ABC において AB = c, BC = a, CA = b とする。

∠ABC = B, ∠BCA = C, ∠CAB = A とする。

 

これらの表記は、正弦定理・余弦定理で頻繁に登場するものです。

今のうちに頭に入れておきましょう。

正弦定理とは

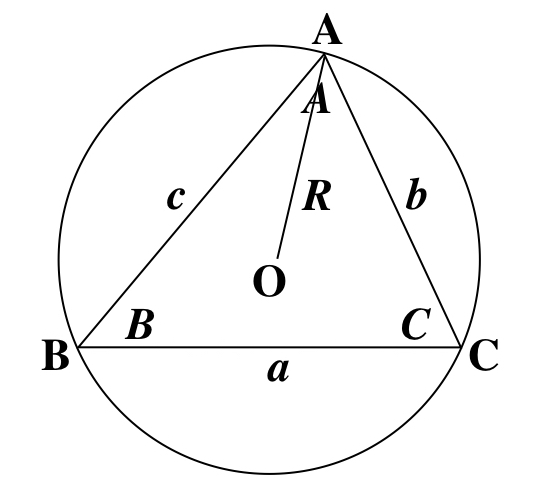
上図のように、△ABC の外接円の半径を R とします。

正弦定理は、その名の通り正弦 (sin) に関する定理で、次のようなものです。

 

 

正弦定理の証明は、こちらの記事で扱っています：

 

例えば a と sinA がわかっているときに、外接円の半径 R を求めることが可能です。

次は、具体的な使い方を見ていきましょう。

正弦定理を用いる問題

ほかの辺の長さを求める

問題

a = 4, A = 30º, B = 105º のとき、c の値を求めよ。

---

ポイント

正弦定理の公式のうち  の部分に着目します。

ここから

・3 つの角度が分かっていれば、3 辺の比が分かる

・3 辺の比が分かっていれば、3 つの角度の正弦の比が分かる

といえますね。これを利用していきます。

 

解答

C = 180º - (A + B) = 180º - 30º - 105º = 45º である。正弦定理より  であるため、

   

外接円の半径を求める

問題

a = 4, A = 30º のとき、R を求めよ。

---

ポイント

今度は外接円の半径の長さを問われています。

与えられている情報量が少ないように見えますが、実はこれで十分です。

(a と A), (b と B), (c と C) のいずれかのペアが分かっていれば、正弦定理から R を求められからです。

 

解答

正弦定理より であるため、

ほかの角度を求める

問題

A = 60º, a = , b = のとき、B, C を求めよ。

---

ポイント

今度は、正弦定理を利用して角度を求めていきます。

三角比の方程式の解き方を思い出しましょう。

今回は、角度の範囲について注意が必要です。

 

解答

正弦定理より であるため、

ここで A = 60º より 0º < B < 180º - A = 120º であるため B = 45º

また C = 180º - (A + B) = 180º - 60º - 45º = 75º

辺の長さと外接円の半径が混在する問題

問題

a = R, C = 10º のとき、B を求めよ。

---

ポイント

今度は角度と辺の長さ、そして外接円の半径が複雑に入り混じった形です。

少しレベルアップしていますが、いつも通り正弦定理で解いていきましょう。

 

解答

正弦定理より であるため

   

0º < A < 180º - C = 170º より A = 30º, 150º

A = 30º のとき B = 180º - (A + C) = 180º - 30º - 10º = 140º

A = 150º のとき B = 180º - (A + C) = 180º - 150º - 10º = 20º

したがって A = 20º, 140º

 

次は「余弦定理」について見ていきましょう。

余弦定理とは

余弦定理は次のようなものです。

余弦 (cos) が登場しているので、余弦定理という名称がついています。

正弦定理と異なり、3 つの式の値は一般的に異なることに注意しましょう。

余弦定理の証明は、こちらの記事で扱っています：

 

余弦定理は

・2 つの辺の長さとその間の角の余弦が分かっているときに、残りの辺の長さを求める

・3 つの辺の長さが分かっているときに、ある角の余弦を求める

といった使い方が可能です。

具体的な問題を見ていきましょう。

余弦定理を用いる問題

残りの 1 辺の長さを求める問題

問題

a = 3, b = 5, C = 60º のとき、c を求めよ。

---

ポイント

最もシンプルな余弦定理の使い方といえます。

初めてこの定理を見た人は、この問題だけでも丁寧に勉強しておきましょう。

 

解答

余弦定理より  であるため、

   

角度の余弦を求め、そこから角度を求める問題

問題

a = , b = , c = 1 のとき、A を求めよ。

---

ポイント

余弦定理からストレートに A を求めることはできません。

まずは A の余弦 cosA を計算し、そこから A を求めます。

 

解答

余弦定理より  であるため、

   

角度を挟む 2 辺のうち片方を求める問題

問題

b = , c = , C = 60º のとき、a を求めよ。

---

ポイント

分かっている角度を挟む 2 辺のうち片方の長さを問われています。

1 つ目の問題と似ていますが、実は少々レベルアップしているのです。

 

解答

余弦定理より  であるため、

   

これを解き、

a > 0 であるため

 

では最後に、正弦定理・余弦定理を用いた応用問題にチャレンジしてみましょう。

正弦定理・余弦定理の応用問題

問題

b = ,  c = 2, B = 30º のとき、a, A, C を求めよ。

---

ポイント

ここまでで学習した正弦定理・余弦定理を用います。

実はこれらの条件だけでは、三角形は一意に決定できません。

そこに気付けると素晴らしいですね。

大きく分けて 2 つの解法があります。

 

解答1 正弦定理を用いる方法

正弦定理より  であるため、

   

B = 30º より 0º < C < 180º - B = 150º であるため、C = 45º, 135º

 

i) C = 45º のとき

A = 180º - (B + C) = 180º - 30º - 45º = 105º

※公式  は後述

ii) C = 135º のとき

A = 180º - (B + C) = 180º - 30º - 135º = 15º

 

以上より , A = 105º, C = 45º または ,  A = 15º, C = 135º

 

 

解答2 余弦定理を用いる方法

余弦定理より  であるため、

   

これを解き、

 

i)  のとき

余弦定理より  であるため、

    よって C = 45º

また A = 180º - (B + C) = 180º - 30º - 45º = 105º

 

ii)  のとき

余弦定理より  であるため、

    よって C = 135º

また A = 180º - (B + C) = 180º - 30º - 135º = 15º

 

以上より , A = 105º, C = 45º または ,  A = 15º, C = 135º

 

今回の問題を解く上で重要な補足事項も述べておきます。

補足１：三角形が一意に決まらない理由

今回の問題では、三角形の形状が一意に決定できませんでした。（答えが 2 つありましたね。）

その理由を考えてみましょう。

 

先ほどの問題では、b = ,  c = 2, B = 30º という 3 つの量が与えられていました。

これがもし b = ,  c = 2, A = 30º だったら、△ABC の形は決定します。

でも今回分かっている角度は B であり、b (CA) と c (AB) で挟まれた長さではありません。

したがって、次のような 2 種類の三角形がありうるのです。

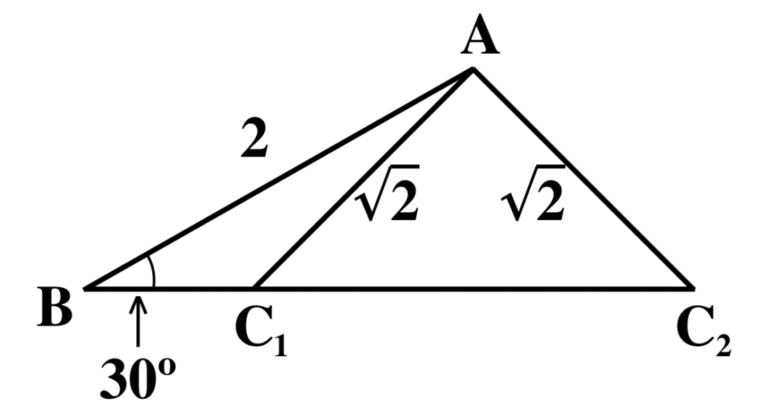
点C が C1 の位置にあるとき となり、C2 の位置にあるとき となります。

これに伴い、答えも複数あったわけです。

補足２：余弦を用いた公式について

解説の中で  というものを用いました。

実はこれ、第一余弦定理という名称がついています。

通常「余弦定理」と呼ばれている などの公式は「第二余弦定理」という名称です。

ただ、名称が紛らわしいので などを単に余弦定理と呼ぶのが通常です。

 

さて、この 公式は見慣れない人が多いと思いますが、証明は思いの外単純です。

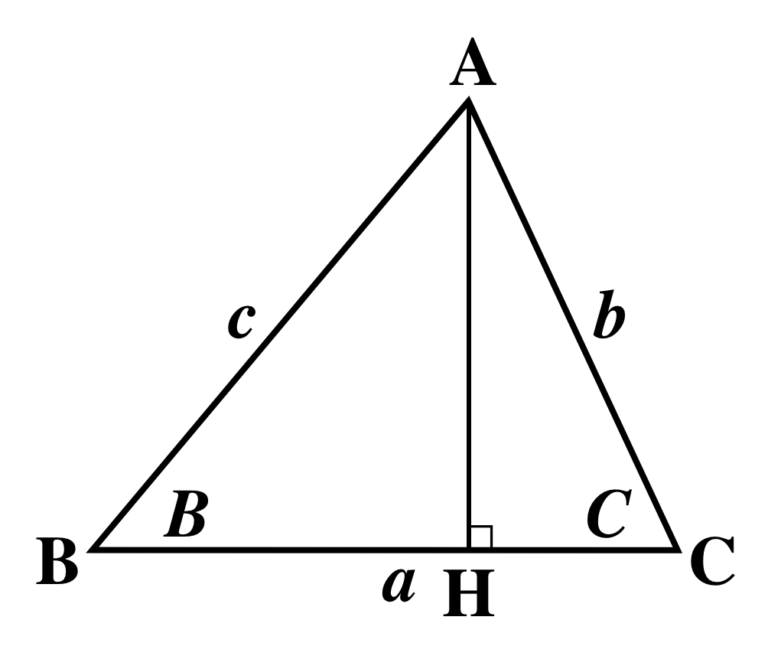
とりあえず鋭角三角形を考えることにします。

上図のように点 H をとりましょう。（点 A から辺 BC に下ろした垂線の足です。）

すると BH = BA cosB = c cosB が成り立ちます。

同様に CH = CA cosC = b cosC です。

以上より a = BC = BH + CH = c cosB + b cosC が示されました。

 

△ABC が鈍角三角形のときも、同様に証明できます。興味のある人は挑戦してみましょう。

まとめ

正弦定理・余弦定理の内容とそれらを用いた代表的な問題の解き方を説明しました。

正弦定理と余弦定理は、「図形と計量」の分野における基本中の基本です。

まず定理の形を正確に覚え、基本的な問題を解けるようにしておきましょう。

 

正弦定理および余弦定理の証明については、別のページで説明しています。