スタクラ情報局
2020.01.06
二次関数の最大値・最小値の求め方を徹底解説！
二次関数の最大値・最小値の求め方
数学 I の山場である二次関数。
特に最大値・最小値の問題は難しいですよね。
というわけで本記事では、https://study-club.jp/二次関数の最大値・最小値の求め方を徹底解説していきます。
学校の授業や定期試験でつまづいてしまった人、試験ではなんとかなったけれど忘れちゃった人…
二次関数をこれから勉強する人・勉強した人、全員必見です！
定義域に制限がないとき
まずは、定義域に全く制限がない二次関数の最大値・最小値を見ていきます。
例題：
二次関数 
の最大値・最小値を求めよ。
解答：
二次関数 のグラフは、
より、軸が直線 x = -1 で頂点が点 (-1, 2) の下に凸の放物線となります。
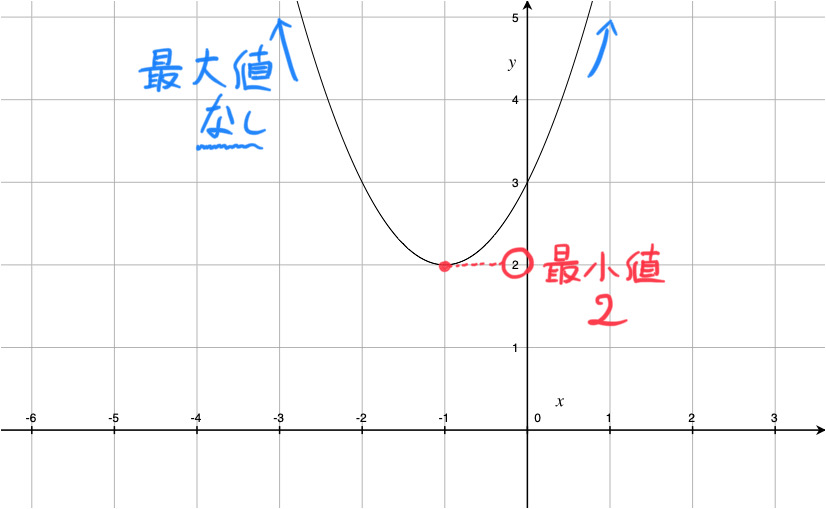
グラフからわかるように、この関数は x = -1 のときに最小値 2 をとります。
また、y はいくらでも大きな値をとるため、最大値は存在しません。
例題：
二次関数 
の最大値・最小値を求めよ。
解答：
二次関数 のグラフは、
より、軸が直線 x = 2 で頂点が点 (2,3) の上に凸の放物線となります。
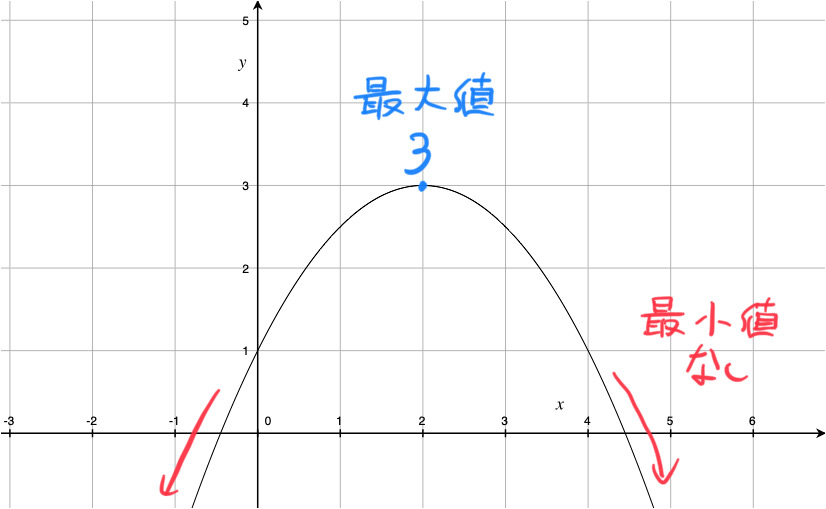
グラフからわかるように、この関数は x = 2 のとき最大値 3 をとります。
また、y はいくらでも小さな値をとるため、最小値は存在しません。
定義域が限られているとき
次に、定義域が制限されている二次関数の最大値・最小値を調べます。
例題：
二次関数 
において、定義域が次の場合の最大値と最小値を求めよ。
またそのときの x の値を求めよ。
(1) 
(2) 
解答：
与えられた二次関数は 
と変形できます。
(1) におけるこの関数のグラフは、下図の放物線の緑線部分です。
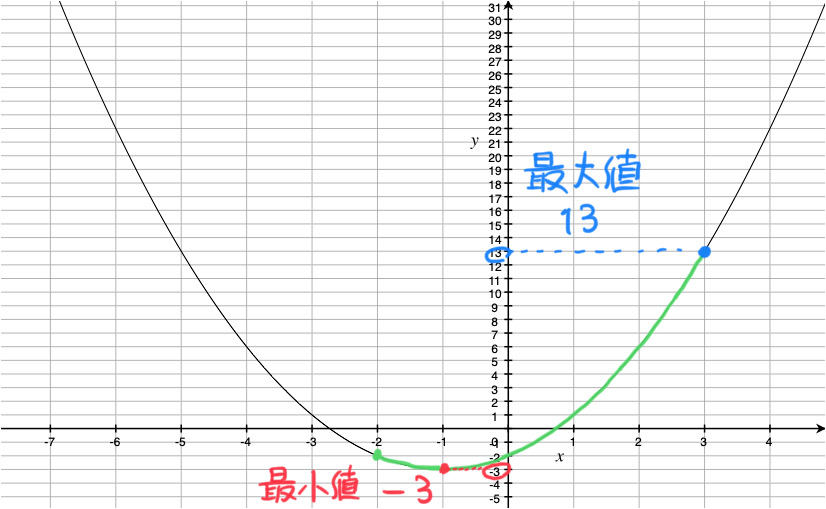
よって、
x = 3 のとき最大値 13
x = =1 のとき最小値 -3
となります。
(2) におけるこの関数のグラフは、下図の放物線の緑線部分です。
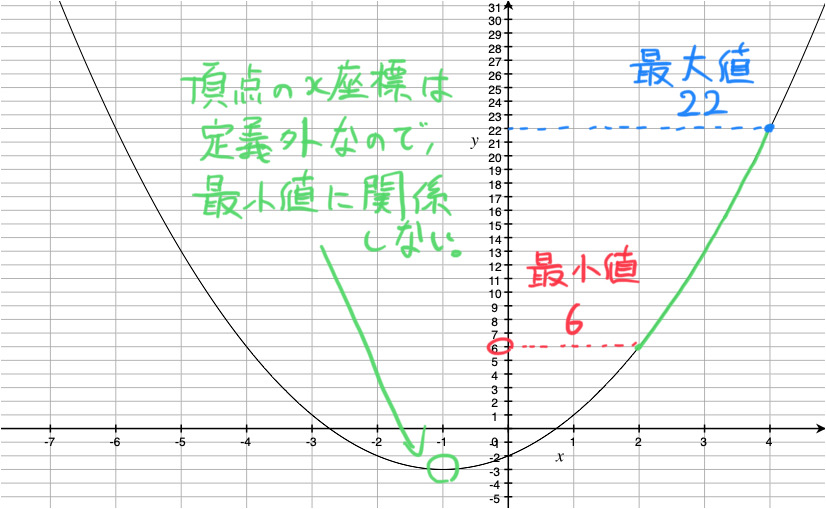
よって、
x = 4 のとき最大値 22
x = 2 のとき最小値 6
となります。
定義域に文字を含む場合の最大値・最小値
これまでは、二次関数・定義域共に文字を含んでいませんでした。
次は定義域に文字を含む場合の最大値・最小値を考えます。
ここから難易度アップ！ じっくり読んでいきましょう。
例題：
のとき、二次関数 
の最小値を求めよ。
解答：
のグラフは、頂点が点 (2, 2) 、軸が直線 x = 2 の下に凸の放物線です。
しかし、a の値によって、
の範囲にグラフの頂点が含まれることもあれば、含まれないこともあるのです。
そこで、a の値によって次のように場合分けしてみましょう。
(i) 
のとき
におけるこの関数のグラフは、下の図の放物線の緑線部分です。
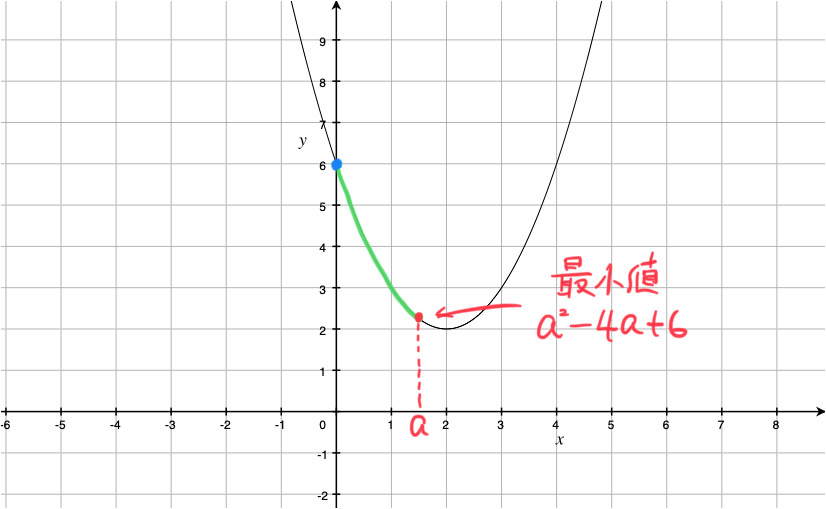
したがって、x = a のとき最小値 
となります。
(ii) 
のとき
におけるこの関数のグラフは、下の図の放物線の緑線部分です。
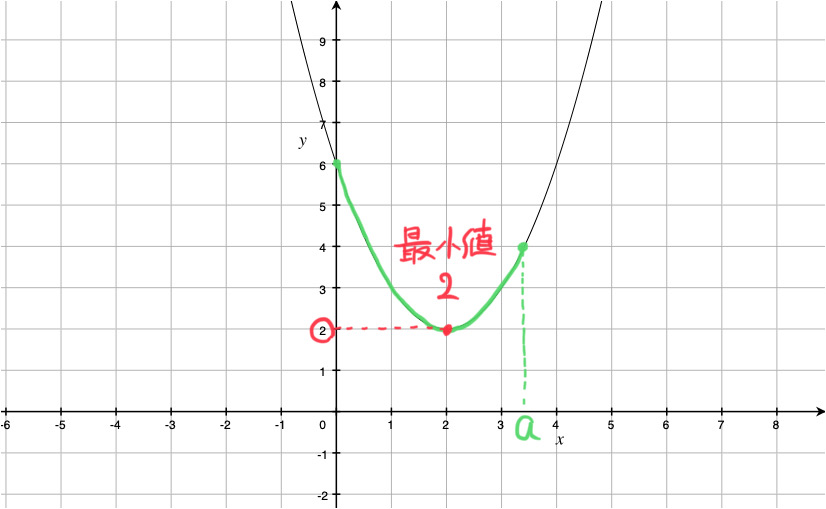
したがって、x = 2 のとき最小値 2 となります。
以上より、
のとき x = a で最小値
のとき x = 2 で最小値 2
が答えです。
軸に文字を含む場合の最大値・最小値
次は、定義域ではなく関数自体（特に軸）に文字を含む場合について考えます。
例題：
のとき、二次関数 
の最小値を求めよ。
解答：
のグラフは、頂点が点 (a, 2) 、軸が直線 x = a の下に凸の放物線です。
ただし、a の値によって 
の範囲に頂点が含まれるか否かが変わります。
そこで、ここでも a の値によって次のように場合分けしましょう。
(i) 
のとき
におけるこの関数のグラフは、下の図の放物線の緑線部分です。
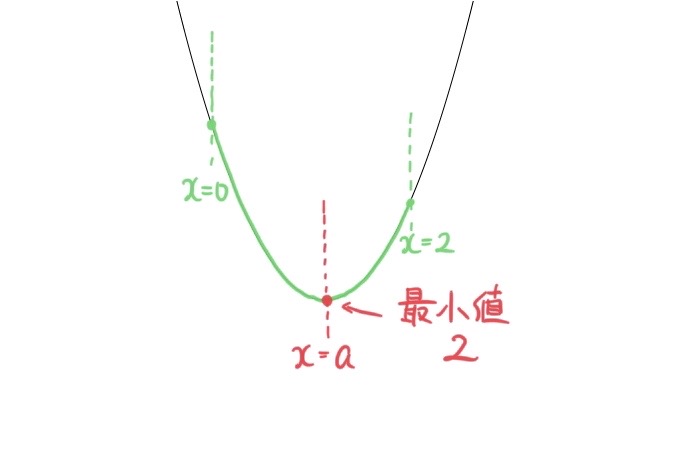
したがって、x = a のとき最小値 2 となります。
(ii) 
のとき
におけるこの関数のグラフは、下の図の放物線の緑線部分です。
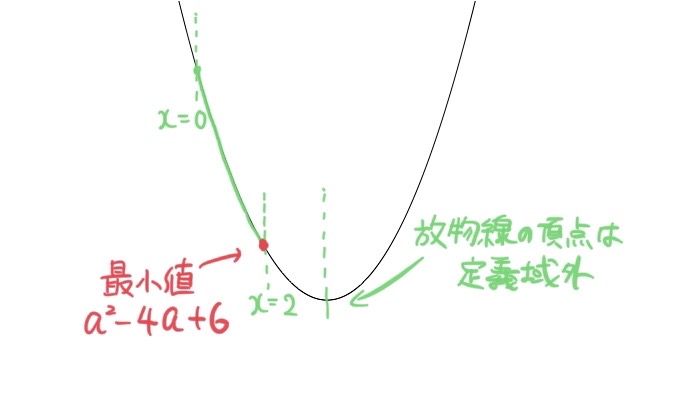
したがって、x = 2 のとき最小値 
となります。
以上より、
のとき x = a で最小値 2
のとき x = 2 で最小値
となります。
最大値・最小値の応用問題に挑戦しよう！
ここまで、二次関数の最大値・最小値について扱ってきました。
まとめとして、次の応用問題に挑戦してみましょう！
応用問題：
二次関数 
の 
における最大値・最小値と、そのときの x の値を求めよ。
解答：
この二次関数は
定義域の始点も終点も定まっていませんが、幅が 2 であることだけは確定しています。
これまでの問題と異なり、複雑な場合分けが必要です。
＜最大値＞
まずは最大値から考えていきましょう。
(i) a+1 < 2 つまり a < 1 のとき
このとき、 におけるこの関数のグラフは、下の図の放物線の緑線部分です。
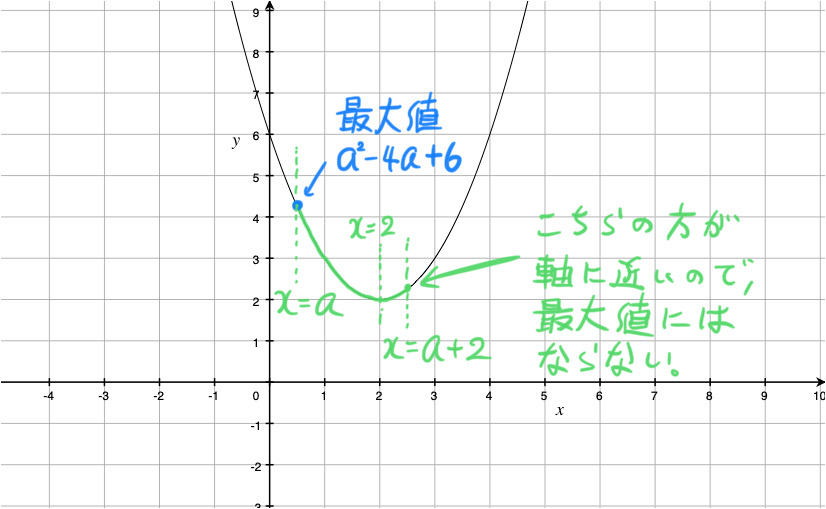
したがって、x = a で最大値 をとります。
(ii) a+1 = 2 つまり a = 1 のとき
このとき、 におけるこの関数のグラフは、下の図の放物線の緑線部分です。
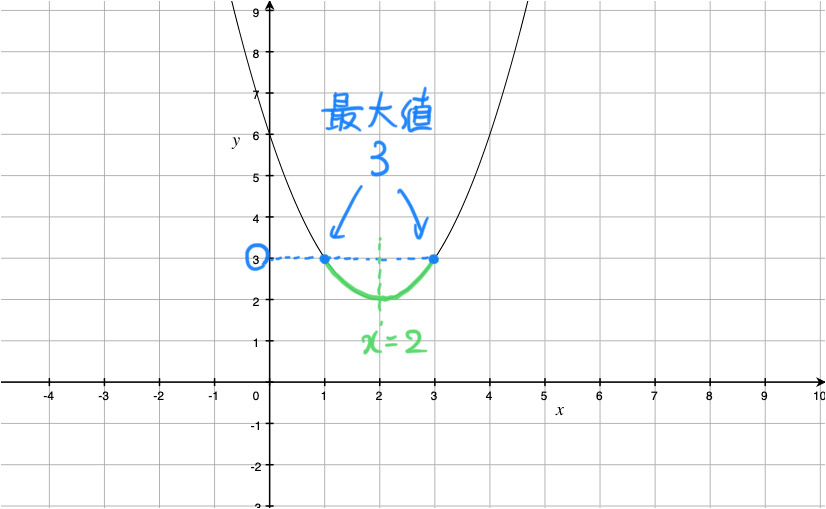
区間 の中心 x = a + 1 と二次関数のグラフの軸の方程式 x = 2 が一致しているので、区間の両端で y は同じ値となるのです。
したがって、x = 1, 3 で最大値 3 をとります。
(iii) a+1 > 2 つまり a > 1 のとき
このとき、 におけるこの関数のグラフは、下の図の放物線の緑線部分です。
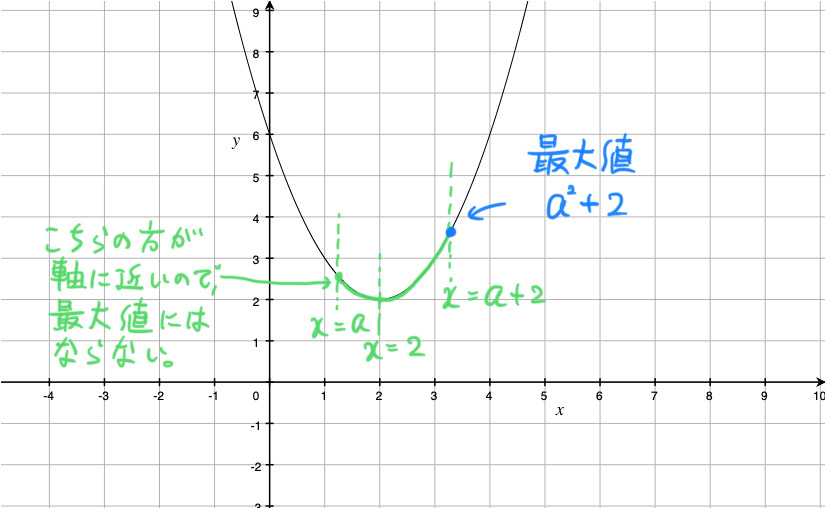
したがって、x = a+2 のとき最大値 
をとります。
＜最小値＞
次に最小値です。
(i) a+2 < 2 つまり a < 0 のとき
このとき、 におけるこの関数のグラフは、下の図の放物線の緑線部分です。
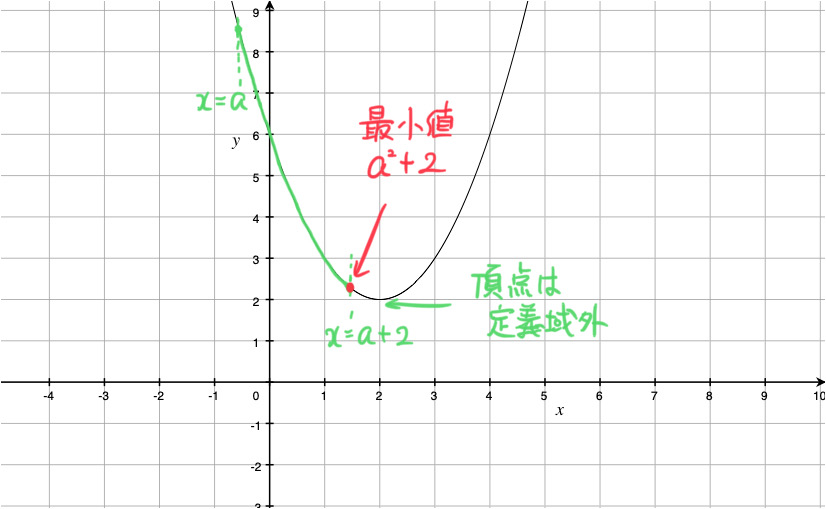
したがって、x = a+2 で最小値 をとります。
(ii) 
つまり 
のとき
このとき、 におけるこの関数のグラフは、下の図の放物線の緑線部分です。
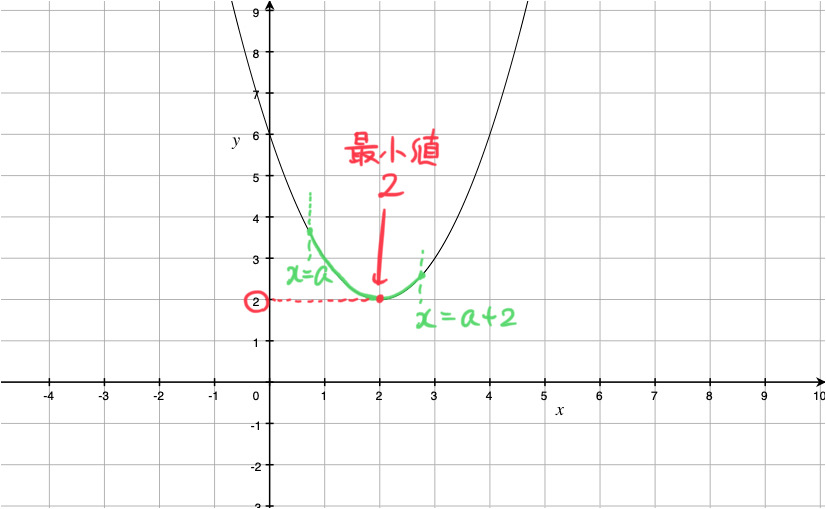
定義域内にグラフの頂点が含まれているので、文句なしでそこが最小点になります。
したがって、x = 2 で最小値 2 をとります。
(iii) 2 < a のとき
このとき、 におけるこの関数のグラフは、下の図の放物線の緑線部分です。
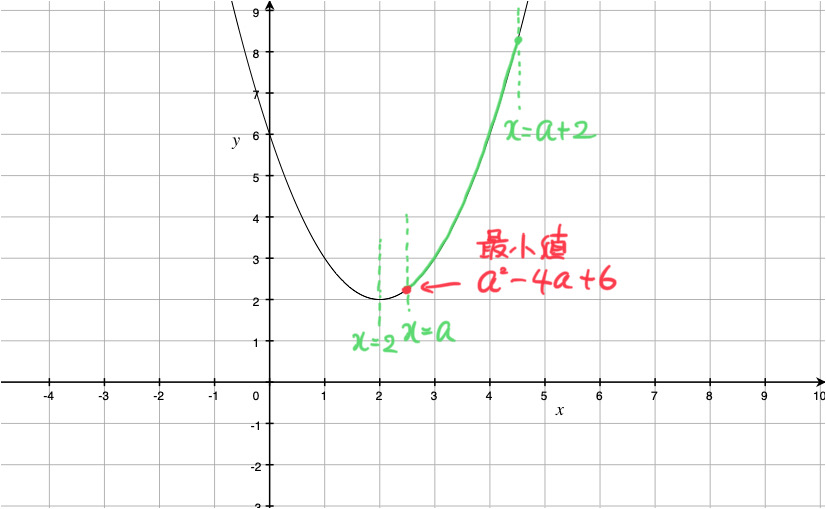
したがって、x = a で最小値 をとります。
以上をまとめると、応用問題の答えは次のようになります：
＜最大値＞
a < 1 のとき、x = a で最大値
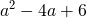
a = 1 のとき、x = 1, 3 で最大値 3
a > 1 のとき、x = a+2 で最大値
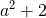
＜最小値＞
a < 0 のとき、x = a+2 で最小値
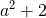
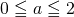- のとき、x = 2 で最小値 2
a > 2 のとき、x = a で最小値
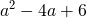
まとめ
二次関数の最大値・最小値について、様々なパターンを解説してきました。
特に重要なポイントを列挙すると次のようになります。
定義域に制限がなくても、最大値・最小値の双方が存在するとは限らない。
定義域に制限がある場合は、「定義域の端点」「頂点」に着目する。
定義域の端点と軸の距離に注意する。
やはりキーワードは「場合分け」でしょう。
なぜ場合分けをしなければいけないのか。
場合分けの境界値はどうなるのか。
これらに注意して、問題を解いてみてください！
