スタクラ情報局
2020.01.15
三角比を用いた面積計算をマスターしよう!
三角比を用いた面積計算
この記事では、三角比を用いた面積計算について説明していきます。
基礎的な面積公式の復習
具体的な問題に入る前に、基本となる面積公式を復習しましょう。
今後考えていく問題は、全て以下の公式をベースとしています。
長方形
最も単純なのは長方形の面積です。
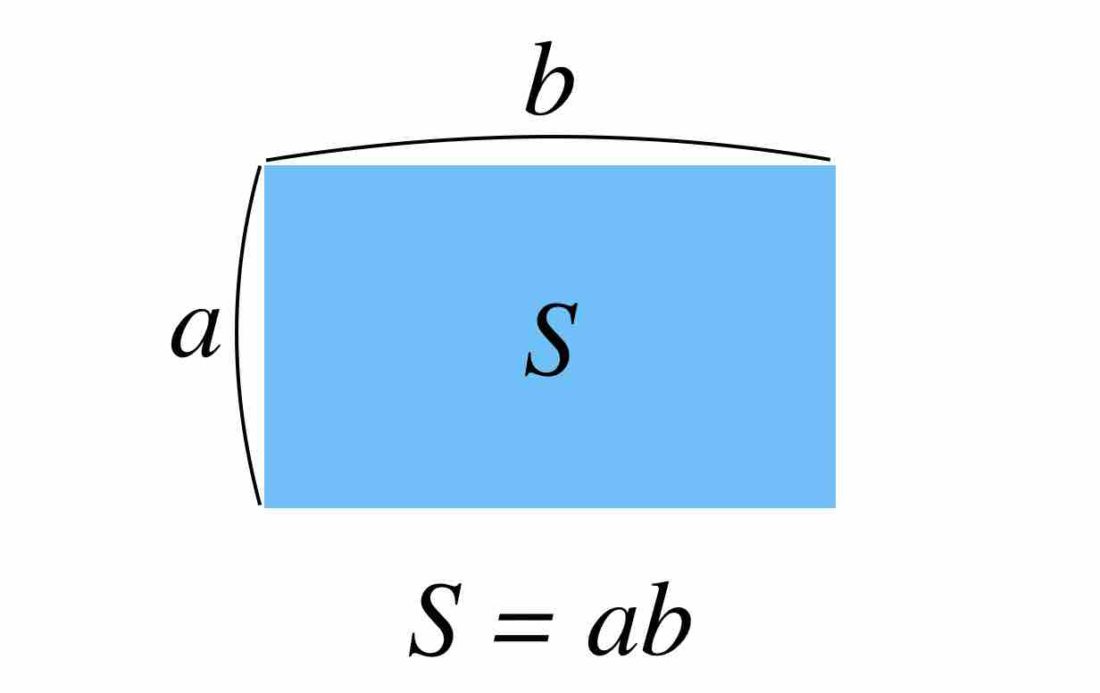
縦の長さが a, 横の長さが b の長方形の面積 S は S = ab となるのでした。
「縦の長さ x 横の長さ = 面積」ということですね。
長方形の面積公式は一見当たり前ですが、今後の面積計算の基礎になるのでここで復習してみました。
三角形
次に、三角形の面積の計算方法を思い出しましょう。
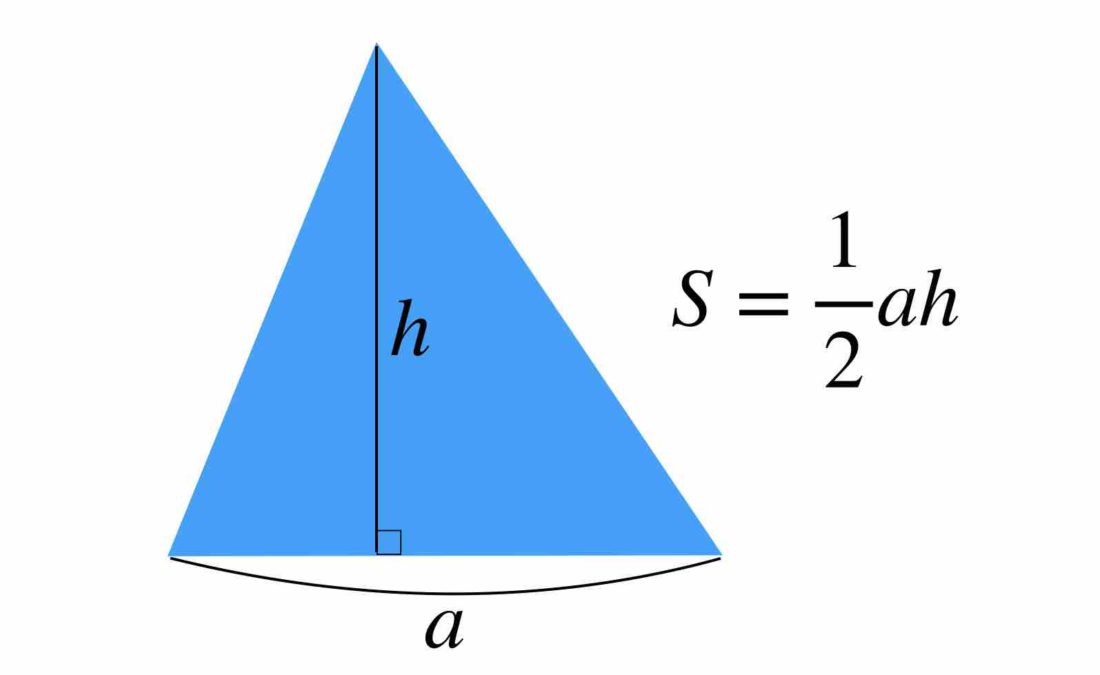
底辺の長さが a、高さが h である三角形の面積 S は S = ah/2 と書けるのでした。
小学生の頃から「底辺 x 高さ ÷ 2」と覚えていたことでしょう。
三角形の面積を三角比で表すと…?
これまで、長方形や三角形の面積公式を復習しました。
ここから主役である三角比の登場です!
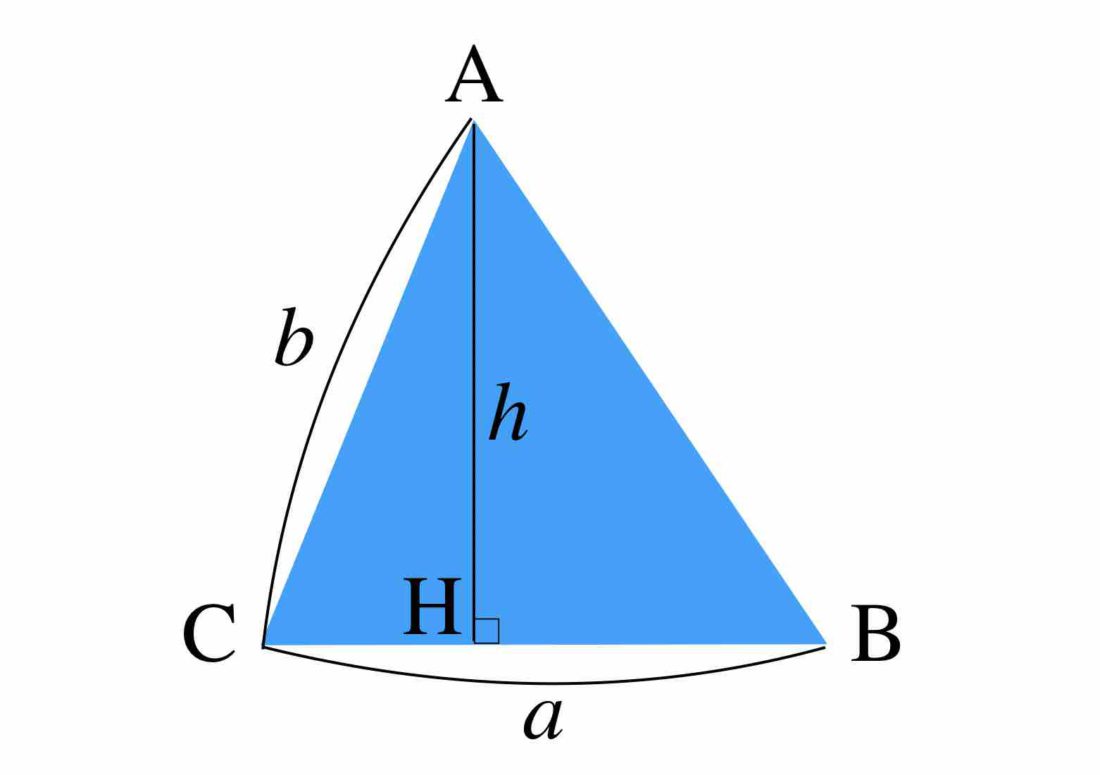
上図のような △ABC を考えましょう。
点 H は、点 A から直線 BC に下ろした垂線の足です。
※特に断りがない場合、a = BC, b = cA, (c = AB) と判断してOKです。
先ほどの面積公式には h (高さ)が含まれているのですが、三角比を用いることで h を用いずに面積を計算します。
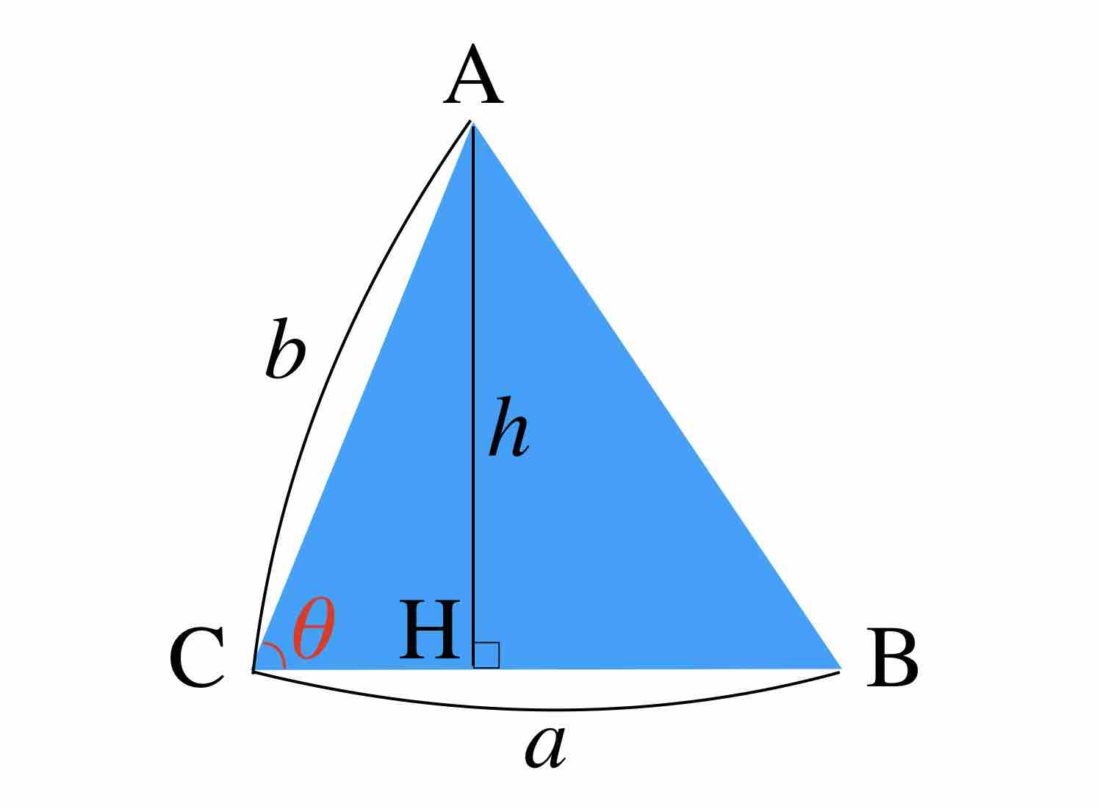
∠ACB = θ とします。(図の赤色の角度です。)
ここで、△ACH に着目して三角比の定義を思い出すと
AH = ACsinθ
が成り立つことがわかります。したがって h = bsinθ となります。
先ほどの三角形の面積公式で h = bsinθ と置き換えると、
![]()
→ ![]()
となり、これが三角比を用いた三角形の面積公式です。
三角比を用いたいろいろな面積問題
では、三角比を用いたいろいろな面積問題を見ていきましょう。
例題1:最もシンプルなパターン
a = 12, b = 4, C = 60º である △ABC の面積 S を求めよ。
図を書いても構いませんが、せっかく三角比で(見た目に依存せずに)解くので図を用いないでやってみましょう。
解答
三角形の面積公式 を用いる。
![]()
三角形の二つの辺と、その間の角度が分かっていれば面積は計算できるという訳ですね。
例題2:三辺の長さが分かっている三角形
a = 10, b = 8, c = 12 であるような △ABC の面積 S を求めよ。
先ほどは「二辺とその間の角」が分かっていましたが、今度は三辺が分かっている場合です。
角度が分かっていないので、先ほどの公式をストレートに用いることはできません。
そこで、次のように工夫していきます。
解答
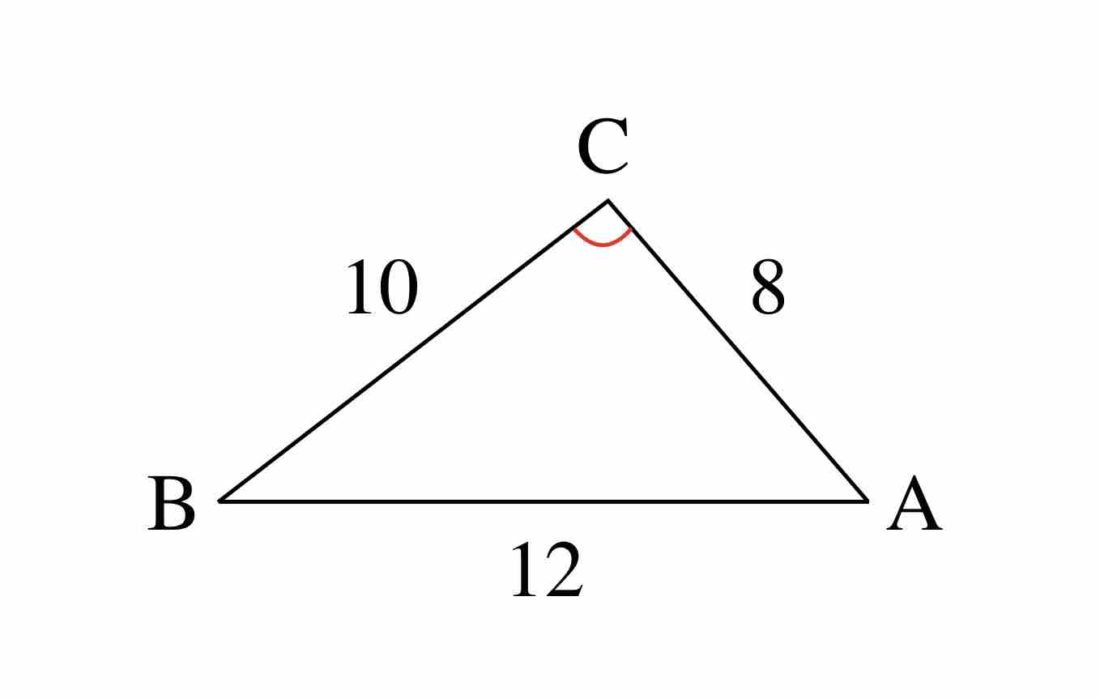
余弦定理より
![]()
であり、0º < A < 180º より sinA > 0 であるから
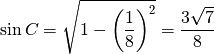
となる。
よって ![]()
例題3:平行四辺形の面積
平行四辺形 ABCD において、対角線 AC, BD の交点を O とする。
AC = 12, BD = 8, ∠AOD = 120º であるとき、平行四辺形 ABCD の面積 S を求めよ。
今度は平行四辺形ですが、やはり三角比を用いた三角形の面積公式を応用して計算します。
解答
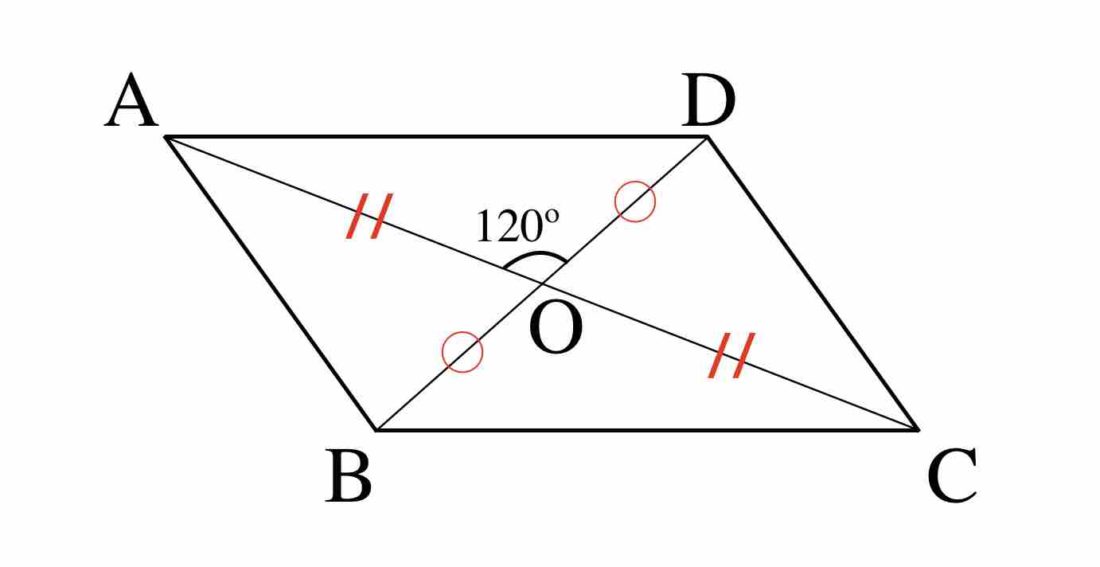
平行四辺形の対角線は、各々の中点で交わるのでした。
したがって AO = CO = 6, BO = DO = 4 となります。
よって、△AOD の面積は
![]()
例題4:台形の面積
AD // BC である台形 ABCD において CD = 5, AC = 7, BC = 8, ∠ADC = 120º とする。
このとき、台形 ABCD の面積 S を求めよ。
だんだん難しくなってきましたね。
台形の面積公式や三角比の余弦定理をフル活用していきます。
解答
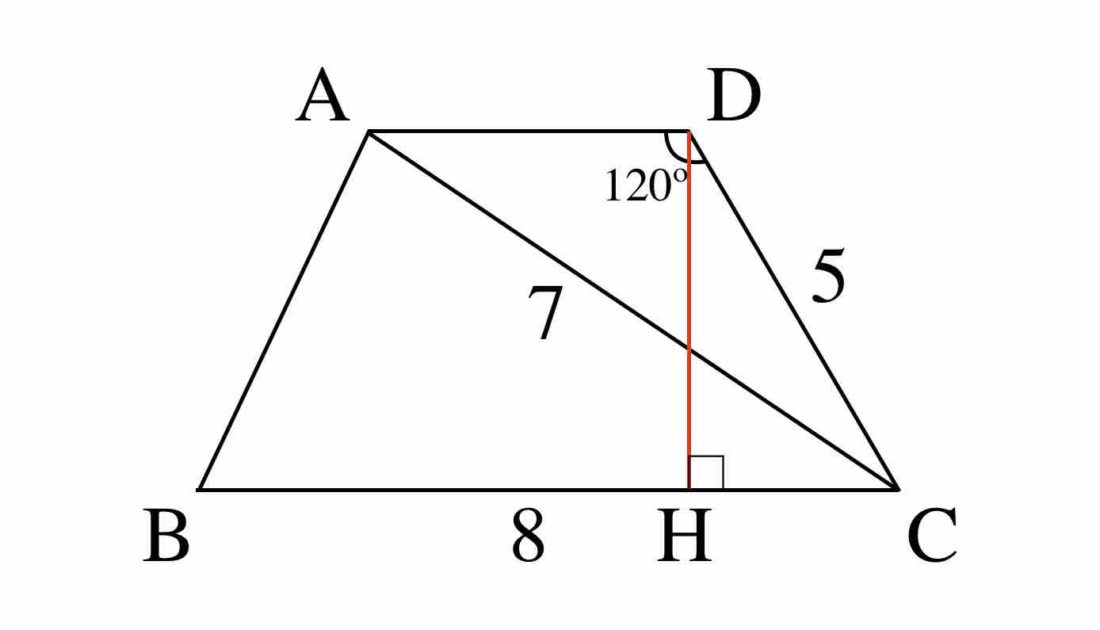
点 D から線分 BC に垂線 DH を下ろす。
AD // BC より ∠BCD = 180º - 120º = 60º
CD = 5 であるため、![]()
AD = x とおく(x > 0)。△ACD で余弦定理より
![]()
![]()
これを解き、x = 3, -8
x > 0 より x = AD = 3
以上より、
![]()
例題5:正多角形の面積
一辺の長さが 1 の正十二角形の面積 S を求めよ。
複雑な図形は、簡単な図形にバラして考えます。
対角線を引き、12 個の三角形に分割しましょう。
各三角形の面積を求める過程で、やはり三角比が登場します。
解答
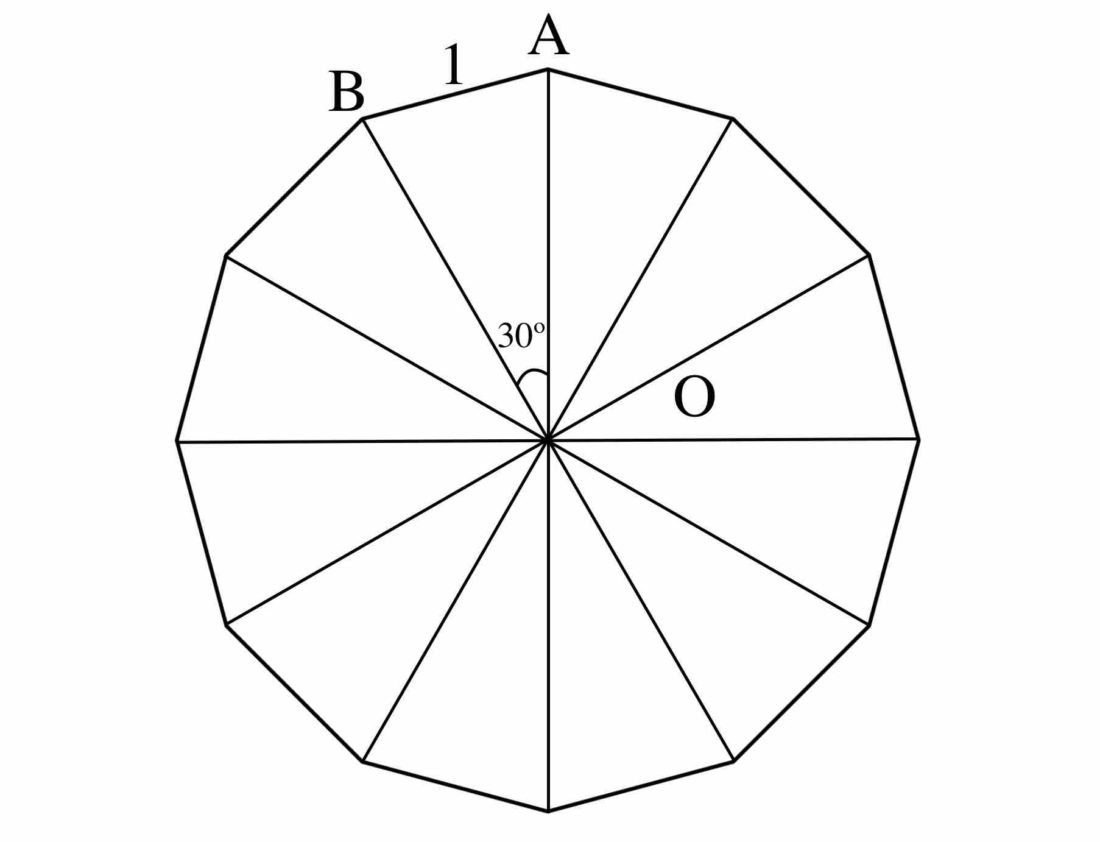
求める面積 S は、△OAB の面積の 12 倍である。
OA = OB = x とすると、△OAB で余弦定理より
![]()
![]()
したがって △OAB の面積は
![]()
以上より
![]()
まとめ:三角形の面積公式をフル活用する
三角比を用いて面積を計算する様々な問題をご紹介しました。
簡単なものから難しいものまで様々でしたが、よーく見てみると、使用している公式は
三角形の面積公式 ![]()
余弦定理 ![]()
くらいとわかります。
つまり、あらゆる問題はこうした基本公式の積み重ねなのです。
この記事でご紹介した問題を攻略する最善の方法は、
三角比の定義
三角比の拡張
正弦定理
余弦定理
三角形の面積公式
などの基礎事項の復習から始めること。
この記事の内容を参考にして、三角比の面積をマスターしてください!

