スタクラ情報局
2020.01.23
三角比の公式をしっかり理解しよう!
三角比の公式をしっかり理解しよう!
この記事では、三角比の定義や基本公式(数学 I)を勉強していきます。
三角比の勉強でつまずいてしまった人は、この記事を読んで勉強しなおしましょう!
三角比の定義(sin, cos, tan)
三角比の定義を改めて勉強します。
「sin って何?」などと聞かれたときに、自分で答えられるようにしておきましょう。
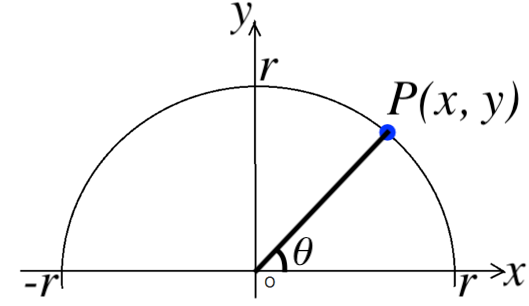
座標平面上で、原点を中心とする半径 r の半円を考えます。
円弧上で、x 軸から角度 θ のところにある点を P (x, y) としたときに、
![]()
![]()
と定義します。
![]()
と定義します。
※数学 I の範囲では ![]() となっていますが、学校によっては
となっていますが、学校によっては ![]() で教えているところもあります。後者の場合、半円ではなくフルの円の図を書きます。
で教えているところもあります。後者の場合、半円ではなくフルの円の図を書きます。
知っておくべき三角比の値
先ほどの三角比の定義に基づき、知っておくべき三角比の値を表にしてみました。
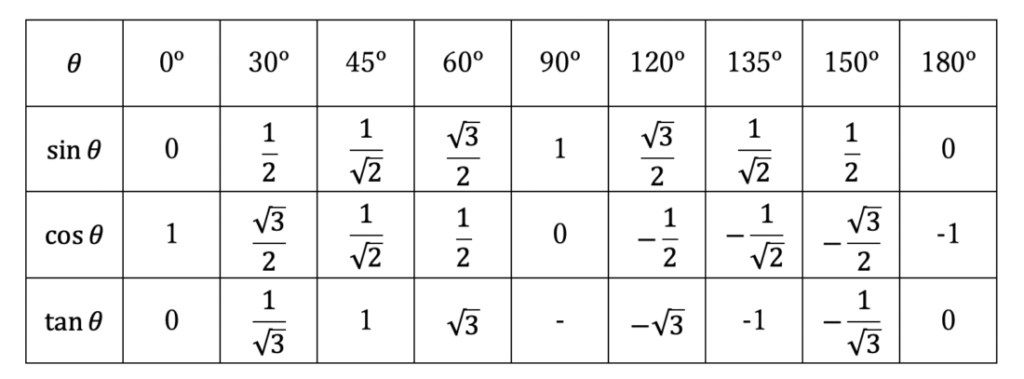
※ 90º での正接(tan)の値は定義されません。無限大とか 0 ではないので注意しましょう。
上表の三角比の値は、今後数学でいくらでも登場します。
図を描くまでもなく一瞬で値を思い出せるよう、特訓しておきましょう。
三角比の公式とその証明
いよいよ本題。
三角比で登場する基本公式を勉強していきます。
相互関係
異なる三角比の間には、次のような関係が成り立ちます。
![]()
![]()
![]()
まず 1 つ目の ![]() ですが、これは三角比の定義を用いて証明することができます。
ですが、これは三角比の定義を用いて証明することができます。
証明)
![]()
右辺を計算して、左辺になるという方針で証明しました。
次に 2 つ目の ![]() ですが、これは三平方の定理を用いると計算できます。
ですが、これは三平方の定理を用いると計算できます。
証明)
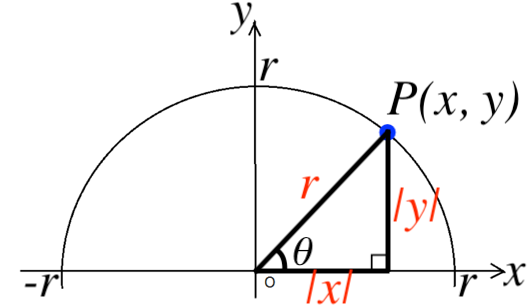
図の直角三角形に着目する。
三辺の長さは r, |x|, |y| であるため、三平方の定理より
![]()
が成り立つ。両辺を ![]() で割ると、
で割ると、
![]()
![]()
となり示された。
3つ目の式は、2つ目の式を変形することで証明できます。
証明)
![]()
の両辺を ![]() で割ると、
で割ると、
![]()
![]()
となり示された。
以上が、三角比の相互関係とその証明でした。
証明も合わせて覚えておくと、覚え間違いを無くせます。
90º - θ, 180º - θ, 90º + θ の三角比
では続いて、90º - θ や 180º - θ の三角比の公式を見ていきます。
まずは公式を一通りご紹介しますね。
<90º - θ>
![]()
![]()
![]()
<180º - θ>
![]()
![]()
![]()
<90º + θ>
![]()
![]()
![]()
以下、これらの公式を証明していきましょう。
90º - θ の公式の証明)
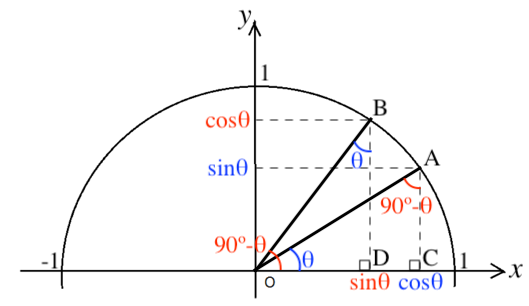
図のように 4 点 A, B, C, D をとる。
このとき、△OAC と △BOD は
OA = OB (円の半径)
∠AOC = ∠OBD = θ
∠ACO = ∠ODB = 90º
であるため合同となる。
よって点 B の座標は B(sinθ, cosθ) となる。
一方 ∠BOD = 90º-θ であるため、点 B の座標は B(cos(90º-θ), sin(90º-θ)) とも表現できる。
両者は全く同じであるため、
sin(90º - θ) = cosθ
cos(90º - θ) = sinθ
が成り立つ。
また、これらより
![]()
がしたがう。
180º - θ の公式の証明)
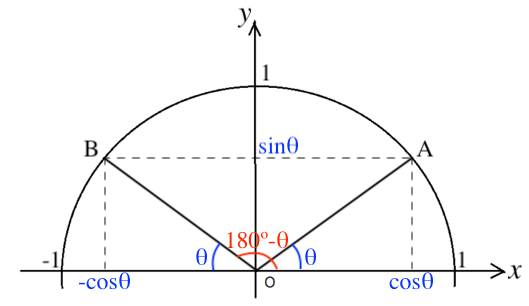
先ほど同様に、単位円を用いて考える。
点 A(cosθ, sinθ) とB(cos(180º-θ), sin(180º-θ)) をとると、線分 AB は x 軸と平行になる。
すると、点 B の座標は (-cosθ, sinθ) と書くこともできる。
したがって
cos(180º-θ) = -cosθ
sin(180º-θ) = sinθ
が成り立つ。
また、これらより
![]()
がしたがう。
90º + θ の公式は、90º - θ と 180º - θ の公式を用いて証明できます。
90º + θ の公式の証明)
![]()
![]()
![]()
まとめ
三角比の定義や基本公式、その証明をご紹介しました。
改めて列挙しておきます。
<相互関係>
![]()
![]()
![]()
<90º - θ>
![]()
![]()
![]()
<180º - θ>
![]()
![]()
![]()
<90º + θ>
![]()
![]()
![]()
様々な公式があり最初は混乱するものですが、証明と共にじっくり勉強すれば知識が正確になります。
丸暗記だと
sin と cos を覚え間違える
マイナスをつけ忘れる
などの危険があるので、証明も欠かさずに理解しましょう。
基本公式は以上ですが、面積計算で登場する公式は次のページで紹介していますので、ぜひご覧ください:
