スタクラ情報局
共通テスト【プレテスト】数学 IA を一挙解説！
共通テストのプレテスト数学 IA の解説
いよいよ次年度入試から，センター試験は「共通テスト」に生まれ変わります。
新しい試験への対策で戸惑う受験生も多いことでしょう。
そこで役立つのが，平成 30 年度に実施された試行調査（プレテスト）です。
新しく始まるテストと同様の問題を想定し，高校生に対して行われたテスト。
それを分析するのが，共通テストのベストな対策といえます。
そこで今回は，共通テスト試行調査（数学 IA）の問題を一気に解説していきます。
なお数学 IIB の問題については下記ページで解説しているので，そちらを参照してください。
平成 30 年度 共通テスト 試行調査について
今回紹介する試行調査（プレテスト）は，独立行政法人大学入試センターが文部科学省の定めた方針により実施したものです。
問題作成の方針を決定すること，そして生徒・学校の情報共有の材料とすることなどを目的としていました。
全国の高校・中等教育学校の生徒たちが，大学を会場として（センター試験・共通テストの本番さながらの環境で）受験しました。
※試行調査自体は，平成 29 年度にも実施されています。
出題のねらいや各問題の正解率等は，全て大学入試センターの HP に掲載されています。
今回扱う平成 30 年度の問題も載っているので，詳細については大学入試センターの HP を参照するようにしてください。
数学IA の問題構成
共通テスト試行調査（プレテスト）の問題構成は次の通りでした。
| 問題 | 分野 | 選択方法 |
| 第 1 問 | 集合と論理，二次関数 | 必答 |
| 第 2 問 | 図形と計量，データの分析 | 必答 |
| 第 3 問 | 確率 | いずれか 2 問を選択肢して解答 |
| 第 4 問 | 整数の性質 | |
| 第 5 問 | 図形の性質 |
数学 I·A 第 1 問 集合と論理・二次関数
〔 1 〕集合と論理
〔 1 〕は「集合と論理」からの出題でした。
(1) 集合や要素の記法，(2) は反例の存在について問うているものです。
＜解説＞
(1)
"1" のみを要素にもつ集合は {1} と書けます。
部分集合であることを記述するためには "⊂" を用いるのでした。
よって (あ) の答えは {1} ⊂ A となります。
(2)
集合 B の要素 x, y で，x + y が有理数となるものを探せばよい。
今回の選択肢の場合，無理数部分が打ち消されればよいので，答えは ①，④ の 2 つとなります。[ ア ] [ イ ]
〔 2 〕２次関数
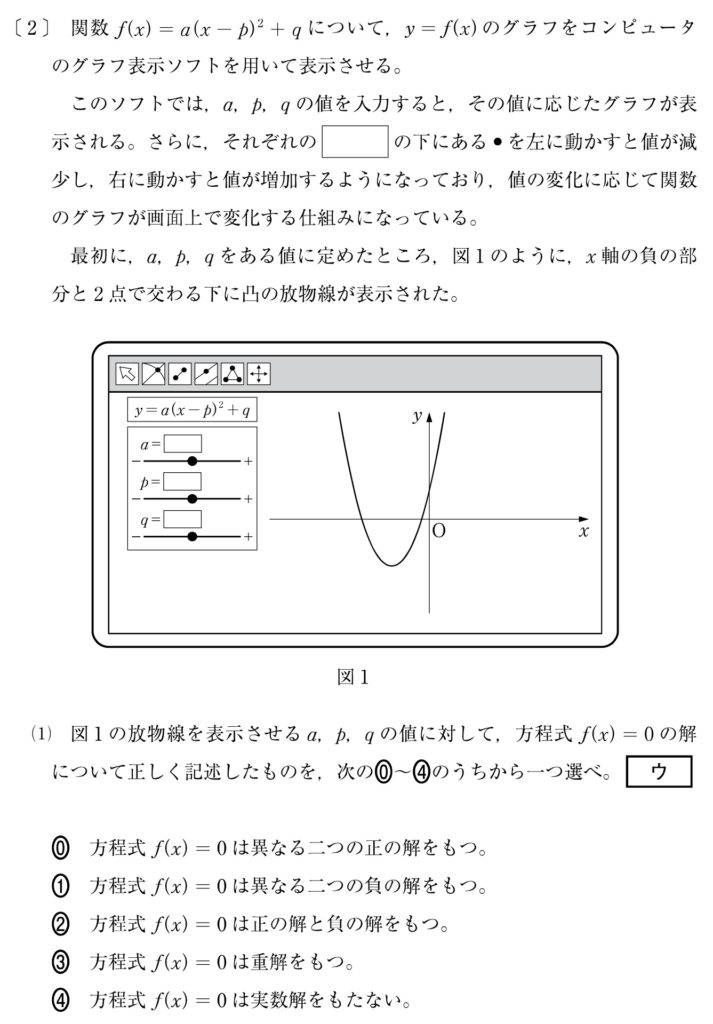
〔 2 〕は二次関数からの出題でした。
二次関数の表示ソフトを操作しているという想定で，各種パラメーターを変化させたときの二次関数のグラフの変化を考えるのがメインテーマです。
＜解説＞
(1)
y = f(x) のグラフは，x 軸と異なる 2 点で交わっていることが図からわかります。
ただし，それだけでは問題は解けません。
x 軸とグラフの交点の x 座標はいずれも負になっています。
したがって，方程式 f(x) = 0 は異なる 2 つの負の解をもち，[ ウ ] は ① となります。
(2)
難しい問題です。
不等式 f(x) > 0 の解が全ての実数となることと，y = f(x) のグラフが x 軸の上側にくることは同値です。
二次関数のグラフが x 軸の上側にくるとき，そのグラフは必ず下に凸になっていなければなりません。
（上に凸だと，いくらでも y の値が小さくなりうるため。）
グラフの頂点も x 軸より上になければなりません。
最初の図では a > 0, p < 0, q < 0 となっており，下に凸ではありますが頂点が x 軸よりも下にあります。
よって q の値を増加させ，グラフ全体を y 軸の正方向に平行移動させれば OK です。
a の値を操作しても，p, q の値が変わらない以上頂点（第３象限）の位置は変わりません。
以上より，不等式 f(x) > 0 の解が全ての実数となりうるような操作は Q のみとなり，[ エ ] は ③ です。
不等式 f(x) > 0 の解が全ての実数となることと，y = f(x) のグラフが x 軸の下側にくることは同値です。
二次関数のグラフが x 軸の上側にくるとき，そのグラフは必ず上に凸になっていなければなりません。
（下に凸だと，いくらでも y の値が小さくなりうるため。）
グラフの頂点も x 軸より下になければなりません。
最初の図では頂点は x 軸よりも下にありますが，下に凸になっています。
a の値を変えないことには，グラフが x 軸の下に来ることはできません。
よって不等式 f(x) > 0 の解が全ての実数となりうるような操作は A のみで，[ オ ] は ① です。
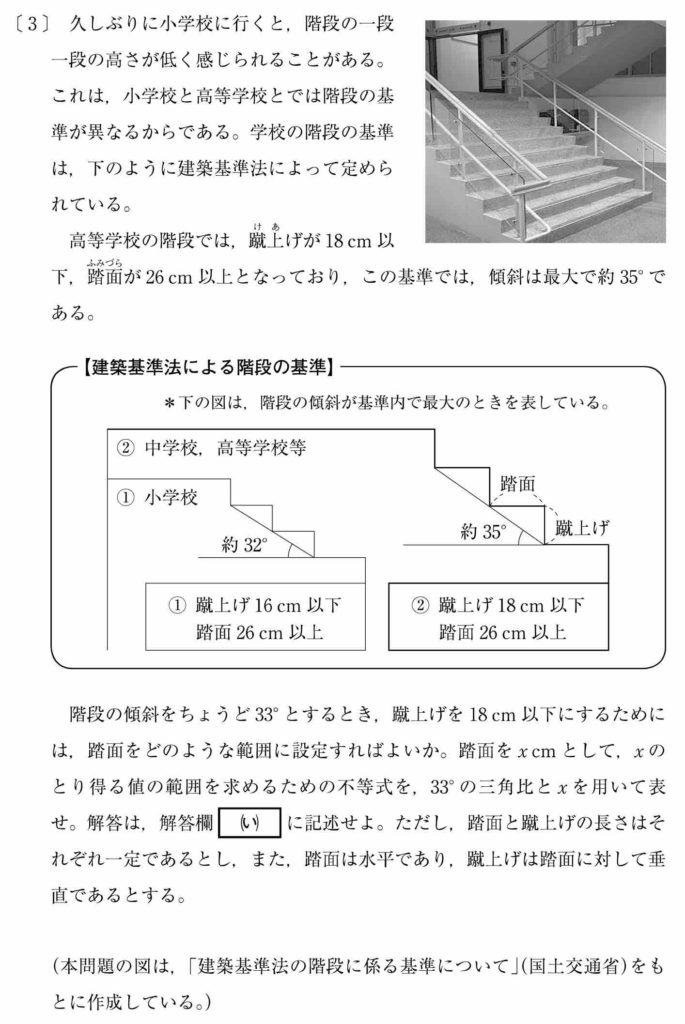
〔 3 〕は共通テスト向けの新傾向を感じさせる問題でした。
「中学校，高等学校等」のルールにしたがって，踏面の値の範囲を求めます。
＜解説＞
踏面を x cm とすると，蹴上は x tan33º となりますね。
これが 18 cm 以下になる必要があるので，
より 
となります。
さらに踏面は 26 cm 以上であるため，両者を合わせて 
が答えです。
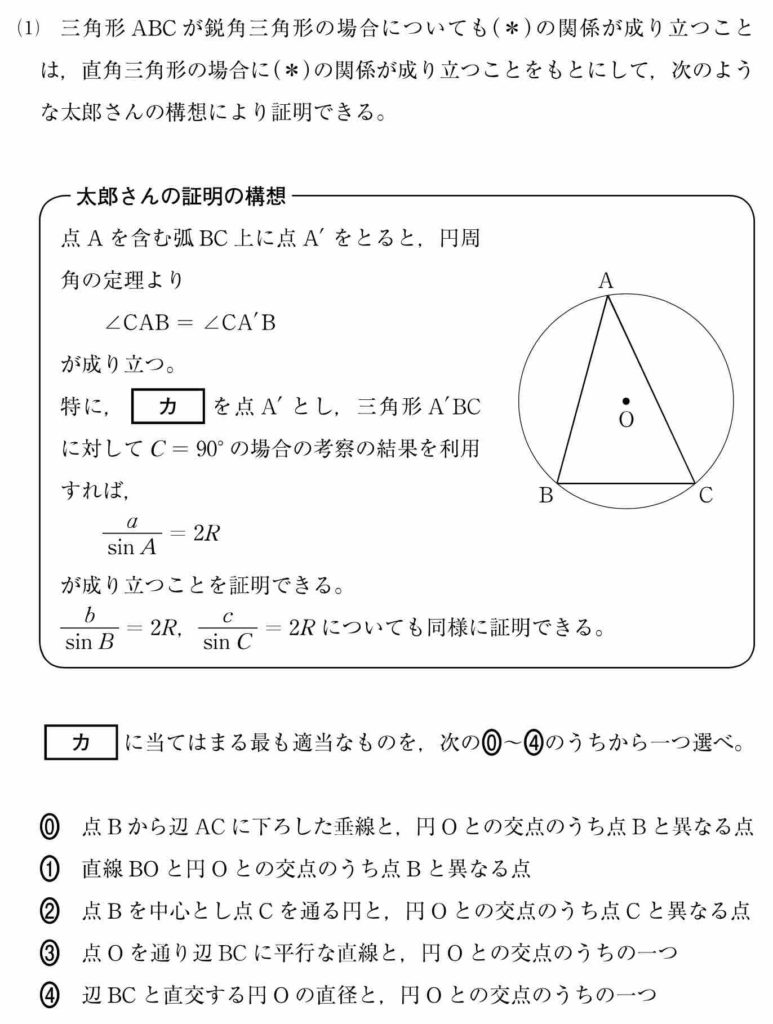
〔 4 〕では正弦定理の証明をしていきます。
＜解説＞
先ほど証明された C = 90º の場合を利用するので，C = 90º になるよう点 A をとらなければいけません。
このとき AB は円の直径になるので，[ カ ] は ① です。
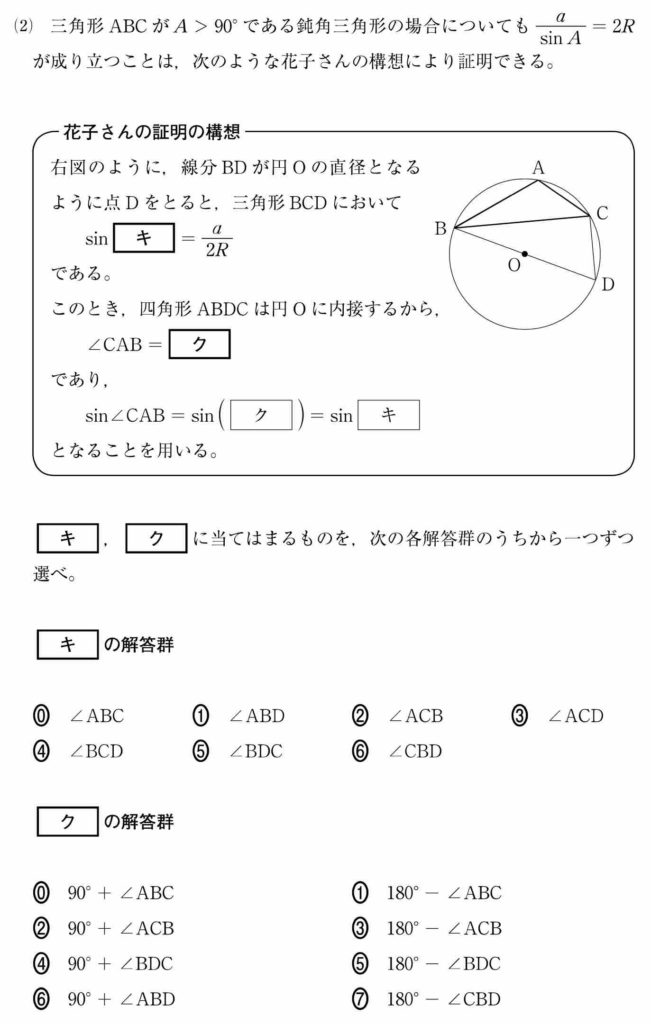
これまで，直角三角形と鋭角三角形における正弦定理は証明できたわけです。
三角形 BCD において BC = a であることに注目すると，∠BDC と BC で正弦定理を用いればいいことがわかります。
[ キ ] の答えは ⑤ となります。
円に内接する四角形で，向かい合う角度の和は 180º になるのでした。
よって ∠CAB = 180º - ∠BDC であり，[ ク ] は ⑤ です。
数学 I·A 第 2 問 図形と計量・データの分析
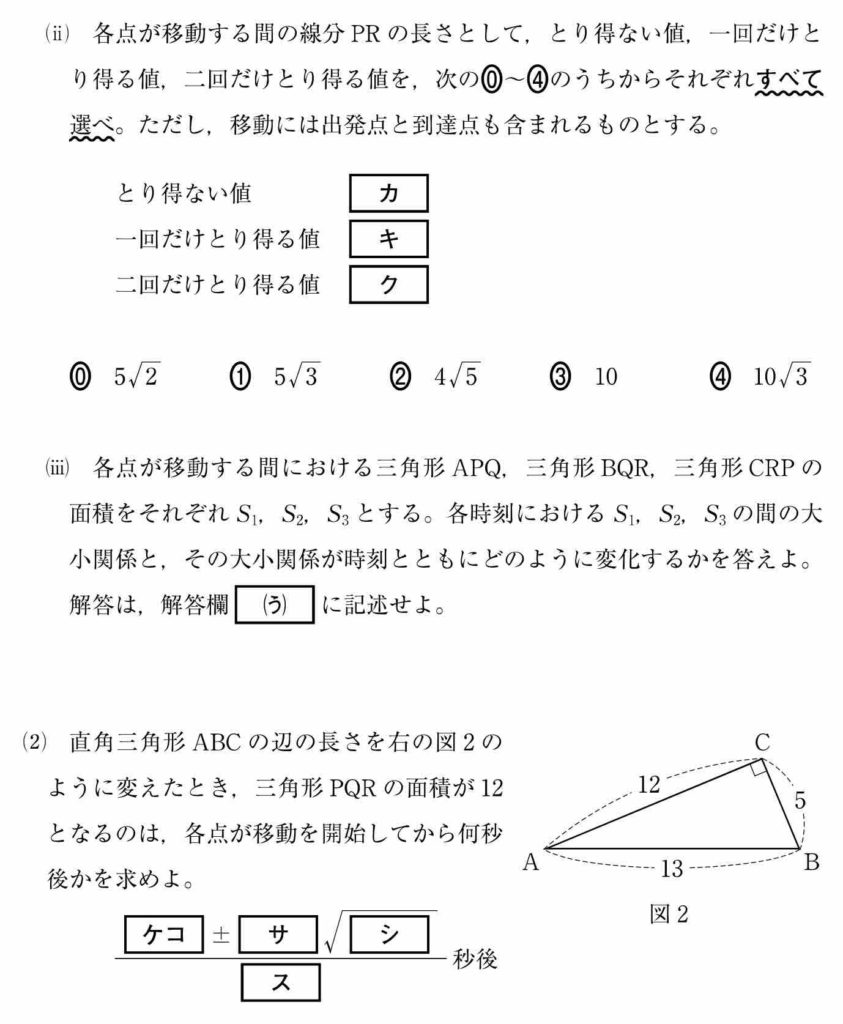
図形分野の応用問題で，センター試験には見られないタイプでした。
センター試験の図形と計量では，基本的に問題図がありませんでしたね。
＜解説＞
Q, R の速さはそれぞれ 2, √3 となります。
(i)
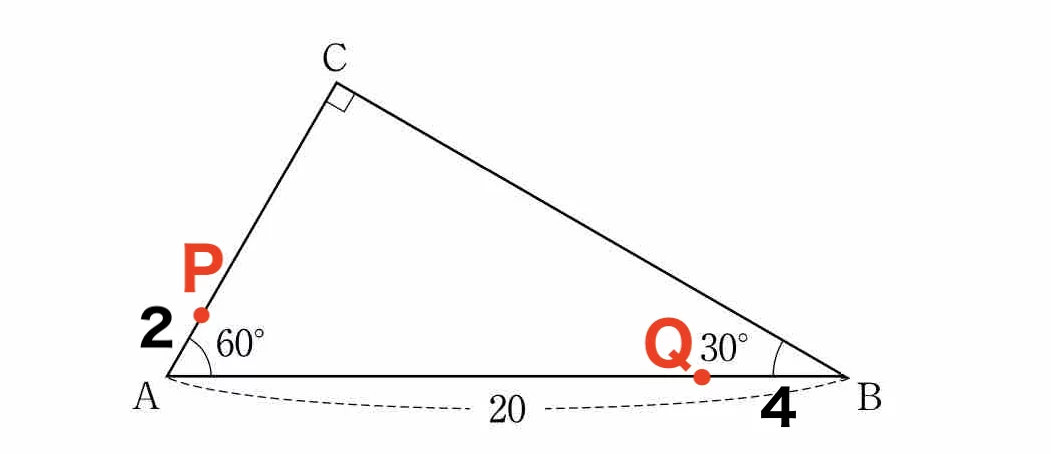
2 秒後の点 P, Q の位置は上図のようになるので，余弦定理より PQ = 2√57 となります。
また △APQ の面積は 
です。
(ii)
各点が出発してから x 秒後の PR の長さは 
となります。
0 ≤ x ≤ 10 のときの二次関数 
の値域は 75 ≤ f(x) ≤ 300 です。
これと選択肢の値（の二乗）と比較します。
各選択肢の値の二乗は順に 50, 75, 80, 100, 300 です。
よって [ カ ] は ⓪，[ キ ] は ①④，[ ク ] は ②③ となります。
(iii)
AP : PC = BQ : QA = CR : RB となっているのがポイントです。
AP : PC = BQ : QA = CR : RB = t : 1 - t とおきます。
△ABC の面積を S とすると 
となり，
も同じ式になります。
したがって常に 
が成り立ちます。（う）
(3)
各点が出発してから y 秒後の △APQ, △BQR, △CRP の面積は
△APQ = 
△BQR =
△CRP =
です。
よって △PQR = 
となり，これが 12 になるような y の値を求めれば OK です。
答えは 
となります。[ ケ ] - [ ス ]
「データの分析」からの出題でした。
ただ，ひたすら計算をするというよりは，相関係数の値について考察するなど，頭を使う問題が多いですね。
＜解説＞
(1)
x の平均は ( 1 + 2 ) ÷ 2 = 1.50 です。よって [ セ ] は ⑧ となります。
x の分散は 
なので，標準偏差は 
となります。よって [ ソ ] は ⑥ です。
y の平均・相関係数も同様となります。
x, y の共分散は 
なので，相関係数は 
となり，[ タ ] は ① です。
(2)
データを ( x, y ) = ( 1, 2 ), ( 2, 2 ) とすると，y の値が全て等しくなるので y の標準偏差が 0 となります。
すると相関係数の式の分母が 0 となってしまうので，相関係数の計算ができません。
したがって [ チ ] は ③ です。
(3)
[ ツ ] は ② です。
問題の前の文章を参考にすると，データの組を ( x, y ) = ( 1, 1 ), ( 2, 2 ), ( 3, 3 ), ( 4, 4 ) とすると相関係数が 1.00 になることが予想され，実際 1.00 になります。
(4)
相関係数は，（向きはともかく）散布図でのデータ点がどれほど直線に近い形で分布しているかを示す数値です。
したがって [ テ ] は ④ となります。
データの組が 2 つしかない場合，（それらが一致していなければ）散布図でのその 2 点を通る直線はただ 1 つに定まります。
したがって相関係数の値は 3 通りに限られるのです。
したがって [ ト ] は ③ となります。
数学 I·A 第 3 問 確率
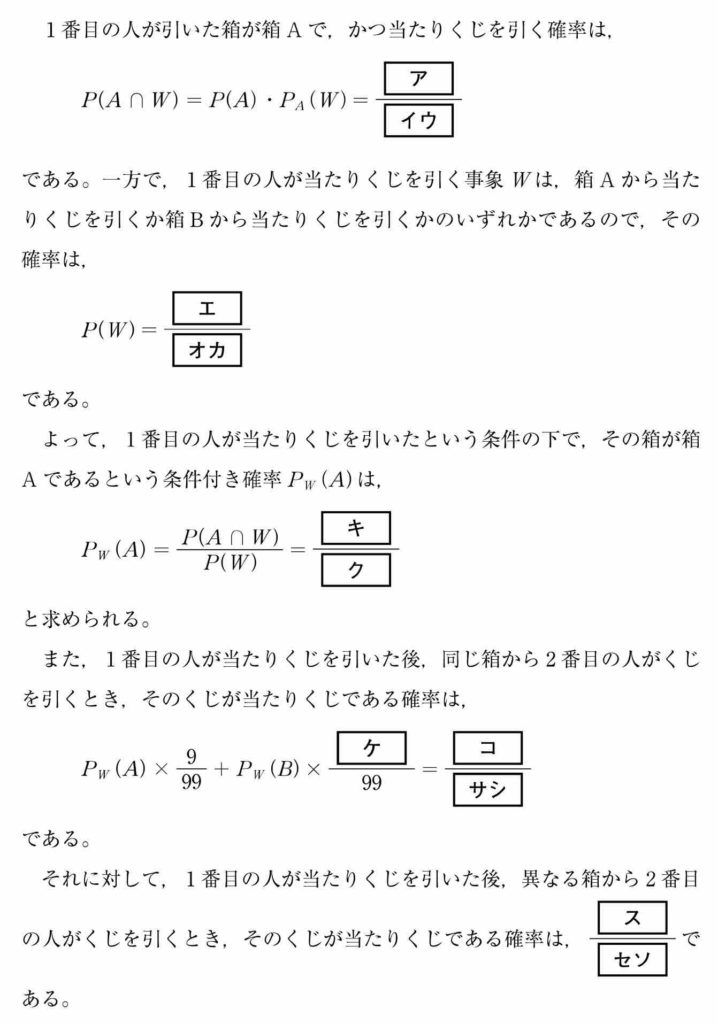
確率・条件付き確率の問題でした。
条件付き確率の定義を思い出しましょう。
＜解説＞
(1)
A をひく確率と，A をひいたうえで当たりを引けばよいので， 
です。[ ア ] - [ ウ ]
同様に
であるため 
となります。[ エ ] - [ カ ]
以上より 
です。[ キ ] [ ク ]
1 番目の人が当たりくじを引いた後，同じ箱から 2 番目の人がくじを引き，それが当たりくじである確率は少々難しいですね。
二人とも A から引く確率と二人とも B から引く確率の和となるので
となります。[ ケ ] - [ シ ]
二人とも箱 B から当たりくじを引く場合，1 番目の人が 5 本中の 1 本目を引いているので，残りが 4 本であるのがポイントです。
同様に考えると，1 番目の人が当たりくじを引いた後，異なる箱から 2 番目の人がくじを引き，それが当たりくじである確率は 
となります。異なる箱なので，分母は 100 であることに注意しましょう。[ ス ] - [ ソ ]
(2)
(1) と同じ手順で確率を計算していくと，1 番目の人が当たりくじを引いた後，同じ箱から 2 番目の人がくじを引き，それが当たりくじである確率は 
となります。[ タ ] - [ ツ ]
今度は同じ箱なので，分母が 100 - 1 = 99 です。
(3)
これまでの結果から，箱 B に入っている当たりくじの本数が 5 本のときは「同じ箱」，7 本のときは「異なる箱」を選択すべきということになります。
したがって 4 本のときは「同じ箱」となるのですが，6 本のときにどうすべきかはこれまでの結果からわかりません。
そこで，(1) (2) と同じように 6 本のときの確率を計算しましょう。
1 番目の人が当たりくじを引いた後，同じ箱から 2 番目の人がくじを引き，それが当たりくじである確率は 
となります。
1 番目の人が当たりくじを引いた後，異なる箱から 2 番目の人がくじを引き，それが当たりくじである確率は 
となります。
であるため，同じ箱を選択すべきということになりますね。
以上より [ テ ] は ① となります。
数学 I·A 第 4 問 整数
第 4 問は，整数分野からの出題。
単なる不定方程式などではなく，天秤ばかりを用いているのが面白いですね。
＜解説＞
- A に X をのせ，B に 3 g の分銅を 3 個のせる
- A に 8 g の分銅を 1 個のせる
- B に 3 g の分銅を 2 個のせる
という操作のあと，A には X と 8 g の分銅 1 個，B には 3 g の分銅 5 個がのっています。
したがって [ ア ] = 1, [ イ ] = 5 となります。
これより M = 7 です。[ ウ ]
(2)
M = 1 のとき，1 + 8 x 1 = 3 x 3 なので [ エ ] は 1 となります。
8 g の分銅 1 個と 3 g の分銅 3 個で 1 g の差を作り出せるので，一般の M については各々の分銅の個数を M 倍すれば OK です。
したがって [ オ ] は ① M, [ カ ] は ④ 3M となります。
(3)
3g の分銅，8 g の分銅を置く皿が逆になっていることに注意します。
(2) の議論を応用すると，例えば ( p, q ) = ( 20, 10 ) とすれば釣り合います。
ここで 3 と 8 は互いに素であるため，p を 8 減らして q を 3 減らしても釣り合いはキープされます。
よって，釣り合うような ( p, q ) の組は ( p, q ) = ( 20 - 8k, 10 - 3k ) と書けます（ k は整数）。
このうち p, q が自然数であり p が最小となるのは k = 2 のときで，このとき ( p, q ) = ( 4, 4 ) となります。[ キ ] [ ク ]
これより方程式 3x + 8y = 20 の解の 1 つは ( x, y ) = ( -4, 4 ) とわかるので，全ての整数解は整数 n を用いて ( x, y ) = ( - 4 + 8n, 4 - 3n ) と書けます。[ ケ ] - [ シ ]
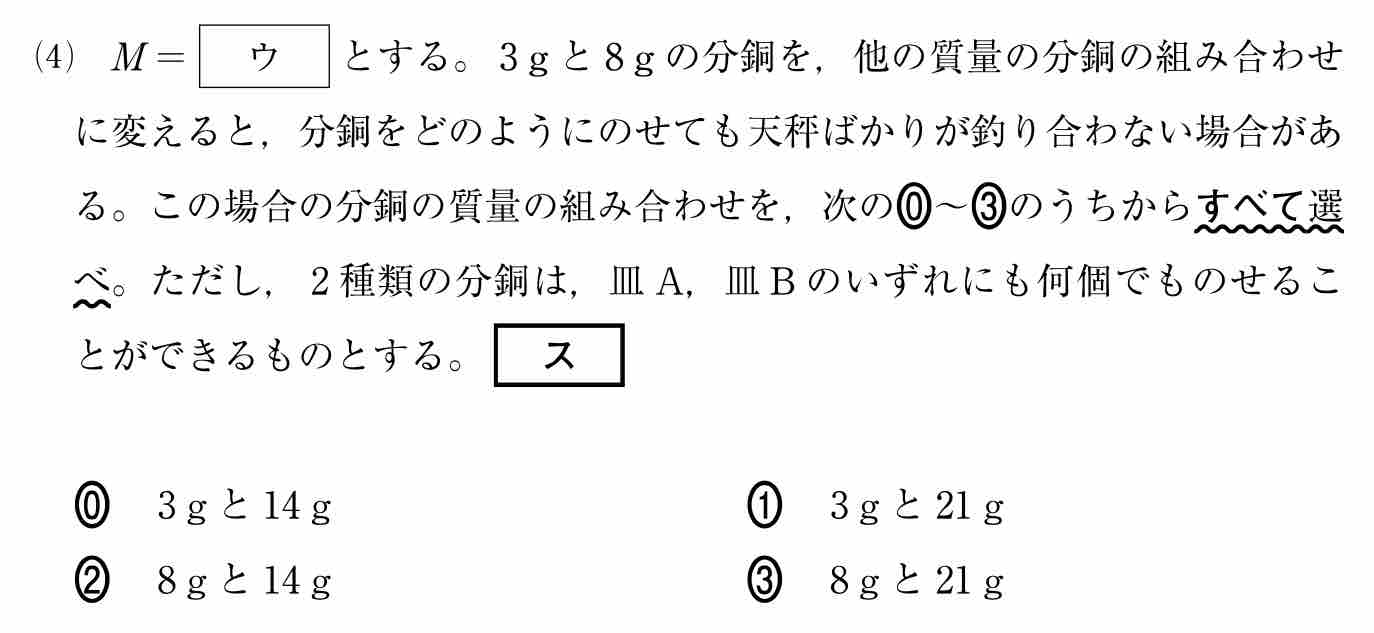
(4)
二種類の分銅の重さ（整数 g ）に 2 以上の公約数があり，その素因数のうち M と互いに素なものがあると，どうやっても天秤が釣り合うことはありません。
そのような分銅の組は ①，② です。[ ス ]
(5)
まだ法則もわからない段階なので，実際に分銅を組み合わせて実験するのがよいでしょう。
自然数 M のうち，非負整数 x, y を用いて 3x + 8y と書けないものは M = 1, 2, 4, 5, 7, 8, 11 の 7 通りです。[ セ ]
最大のものは M = 11 ですね。[ ソ ] [ タ ]
後半は読解力も要求されるので難しかったかもしれません。
問題に記されている考え方に従うと，非負整数 x, y を用いて 3x + 2018y と書ける自然数のうち
・3 で割り切れる最小のものは 3
・3 で割って 1 余る最小のものは 2018
・3 で割って 2 余る最小のものは 2018 x 2 = 4036
となります。裏を返せば，非負整数 x, y を用いて 3x + 2018y と書けない自然数のうち
・3 で割って 1 余る最小のものは 2018 - 3 = 2015
・3 で割って 2 余る最小のものは 2018 x 2 - 3 = 4033
であるため，非負整数 x, y を用いて 3x + 2018y と書けない自然数の最大値は 4033 となります。[ チ ] - [ ト ]
数学 I·A 第 5 問 図形の性質
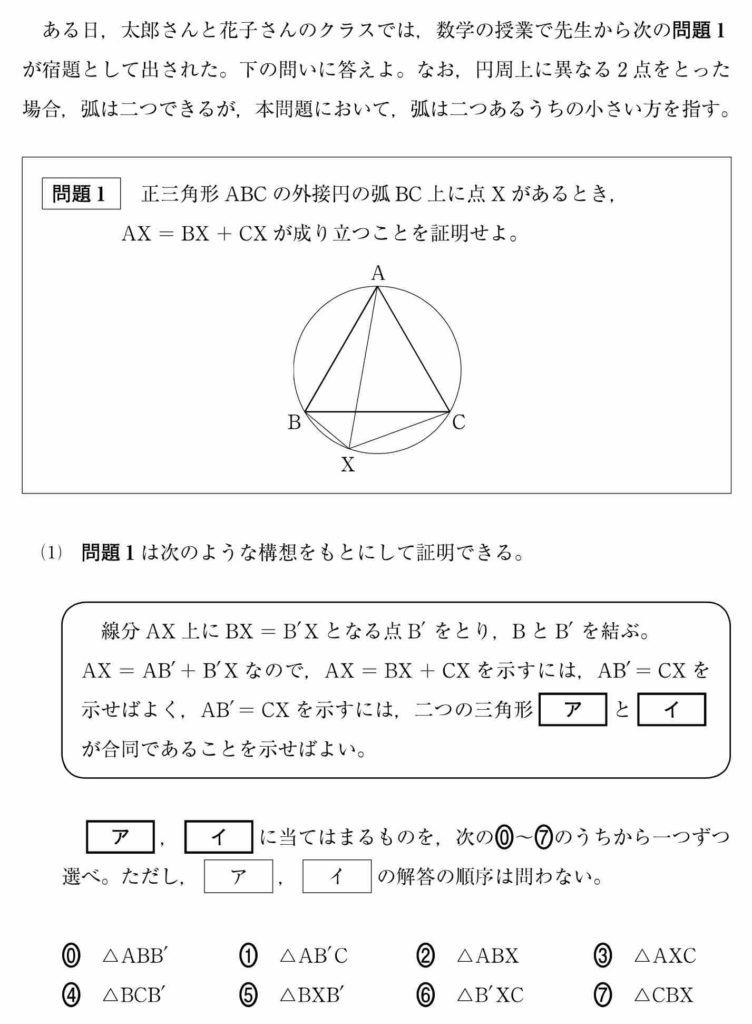
いわゆる「フェルマー点」について，いくつかのステップに分けて考えていく大問でした。
誘導に乗っていくことで，フェルマー点の位置がわかります。
＜解説＞
(1)
AB' = CX であることを証明したいので，その辺が登場する三角形を選択します。
AB', CX が登場するだけでなく，対応する辺が AB', CX になっていなければならないのがポイントです。
よって ⓪ △ABB', ⑦ △CBX が合同であることを証明すれば OK です。[ ア ] [ イ ]
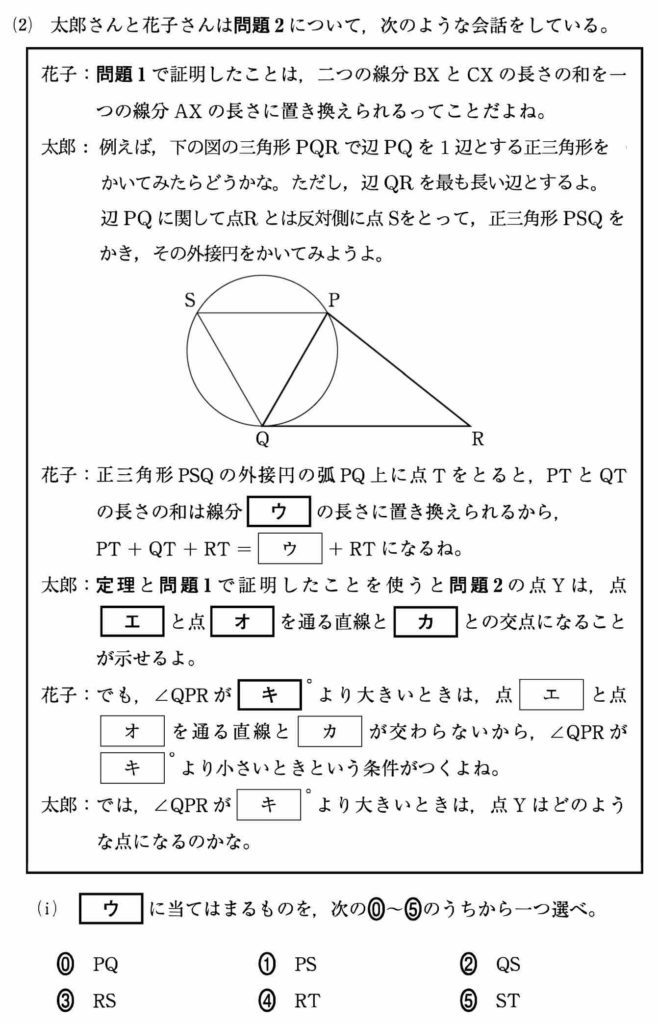
(2)
(i)
まず [ウ] ですが，(1) の結果を利用すると PT + QT = ST （⑤）となります。
(ii) (iii)
したがって PT + QT + RT = ST + RT となります。
ここで ST + RT は S, R を始点・終点とする折れ線の長さです。
よってこれが最小となるような点（問題 2 の点 Y）は，点 R, 点 S を通る直線と弧 PQ の交点です。
したがって [ エ ] = ②，[ オ ] = ③，[ カ ] = ③ です。
(iv)
直線 RS と弧 PQ が交わらないギリギリの状態を考えます。
このとき，直線 RS が弧 PQ の端点 P を通っていることになりますね。
三点 R, P, S は同一直線上にあるので ∠SPR = 180º であり，このとき ∠QPR = 180º - 60º = 120º です。[ キ ] = ④
(v)
これまでの議論のまとめです。（引き続き，QR が最も長いものとしましょう。）
結局 ∠QPR が 120º より小さければ，PT + QT + RT が最小となる点 T （これを特別に Y とよぶ）は弧 PQ 上にあるのでした。
このとき ∠PYQ = 120º となります。
今回は辺 PQ を一辺とする正三角形を作りましたが，△PQR が鋭角三角形であれば辺 QR, RP についても全く同様の議論ができるため，点 Y は
・∠PYQ = 120º
・∠QYR = 120º
・∠RYP = 120º
を全て満たすことがわかります。
したがって [ ク ] は ③ となります。
∠QPR が 120º より大きい場合を考えるのは非常に難しいですが，∠QPR が小さい方から 120º に近づいていく様子を考えるとわかりやすいかもしれません。
いま考えている点 Y は
・∠PYQ = 120º
・∠QYR = 120º
・∠RYP = 120º
をみたしているので，∠QPR が小さい方から 120º に近づいていくと点 Y は点 P に接近していきます。
∠QPR が 120º より大きい場合，点 Y は点 P と一致することが予想できますね。
論理的に点を特定するのは難しいのですが，以上の考え方より答えは ⑥「点 Y は，△PQR の三つの辺のうち，最も長い辺を除く二つの辺の交点である。」 となります。[ ケ ]
まとめ
平成 30 年度実施の，共通テスト試行調査（プレテスト）数学IA の解説でした。
これまでのセンター試験と比較すると，
・記述式で解答する問題があった（注：次年度入試では記述式はなし）
・会話文を用いた問題が出題されている。
・図表が多く用いられている。
・計算量が大きく減少している。
といった特徴があります。
何も考えずに前から順番に計算していけばよい，というわけではないので注意が必要です。
会話・問題文を注意深く読み，誘導にうまく乗るのが高得点獲得のポイントです。
とはいえ，共通テストの問題の演習は数学 IA の学習が終わった後でよいでしょう。
教科書レベルの内容に抜けがあるうちは，地道な勉強を忘れずに！
共通テストに関連する情報は，例えば下記のページにまとめられています。
必要に応じて参照してください。
