スタクラ情報局
共通テスト【プレテスト】数学 IIB を一挙解説！
共通テストのプレテスト数学 IIB の解説
いよいよ次年度入試から，センター試験は「共通テスト」に生まれ変わります。
新しい試験への対策で戸惑う受験生も多いことでしょう。
そこで役立つのが，平成 30 年度に実施された試行調査（プレテスト）です。
新しく始まるテストと同様の問題を想定し，高校生に対して行われたテスト。
それを分析するのが，共通テストのベストな対策といえます。
そこで今回は，共通テスト試行調査（数学 IIB）の問題を一気に解説していきます。
なお数学 IA の問題については下記ページで解説しているので，そちらを参照してください。
平成 30 年度 共通テスト 試行調査について
今回紹介する試行調査（プレテスト）は，独立行政法人大学入試センターが文部科学省の定めた方針により実施したものです。
問題作成の方針を決定すること，そして生徒・学校の情報共有の材料とすることなどを目的としていました。
全国の高校・中等教育学校の生徒たちが，大学を会場として（センター試験・共通テストの本番さながらの環境で）受験しました。
※試行調査自体は，平成 29 年度にも実施されています。
出題のねらいや各問題の正解率等は，全て大学入試センターの HP に掲載されています。
今回扱う平成 30 年度の問題も載っているので，詳細については大学入試センターの HP を参照するようにしてください。
数学IIB の問題構成
共通テスト試行調査（プレテスト）の問題構成は次の通りでした。
| 問題 | 分野 | 選択方法 |
| 第 1 問 | 三角関数，指数・対数関数 | 必答 |
| 第 2 問 | 図形と方程式 | 必答 |
| 第 3 問 | 統計 | いずれか 2 問を選択肢して解答 |
| 第 4 問 | 数列 | |
| 第 5 問 | ベクトル |
数学IIB 第 1 問 三角関数，指数・対数関数
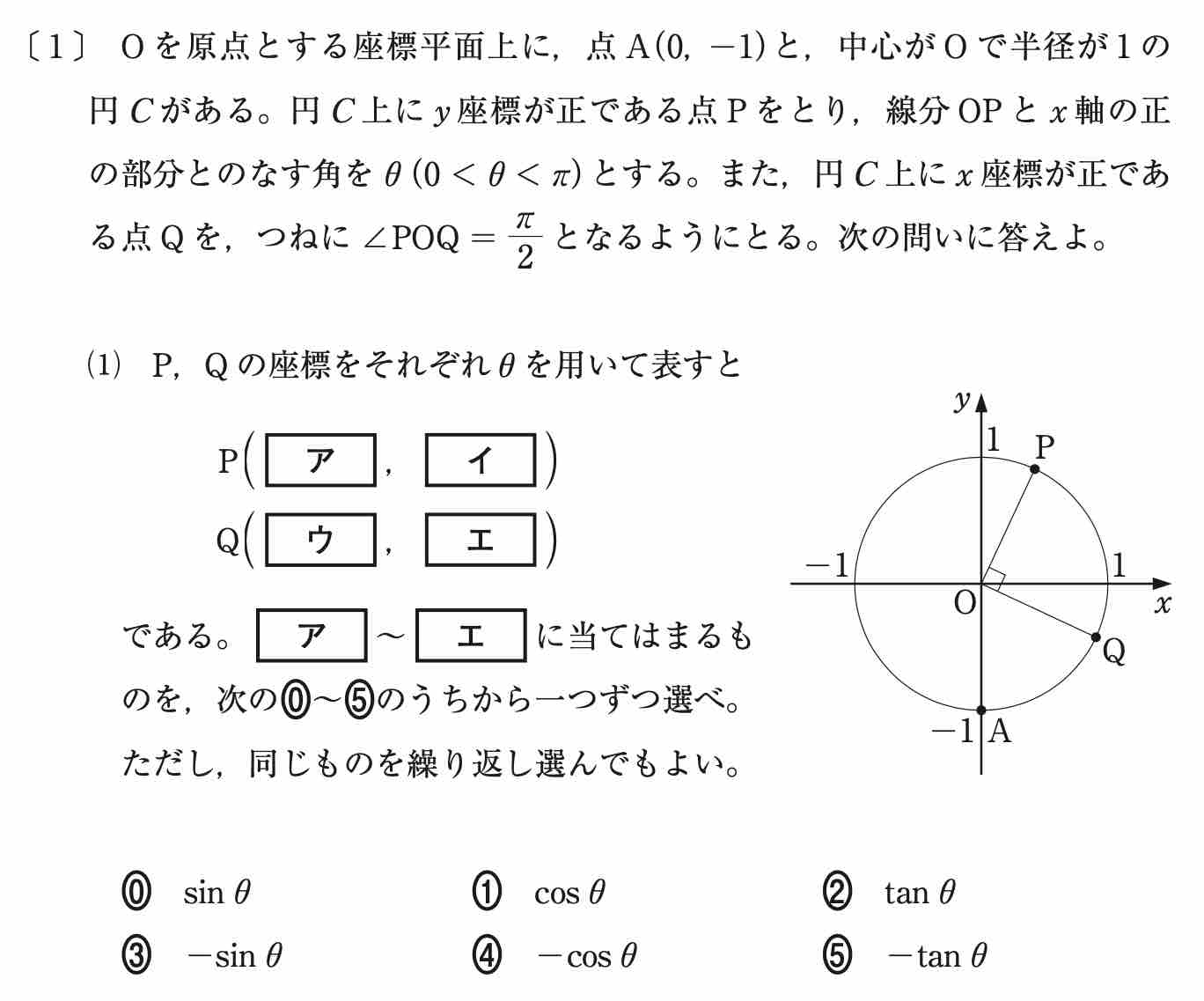
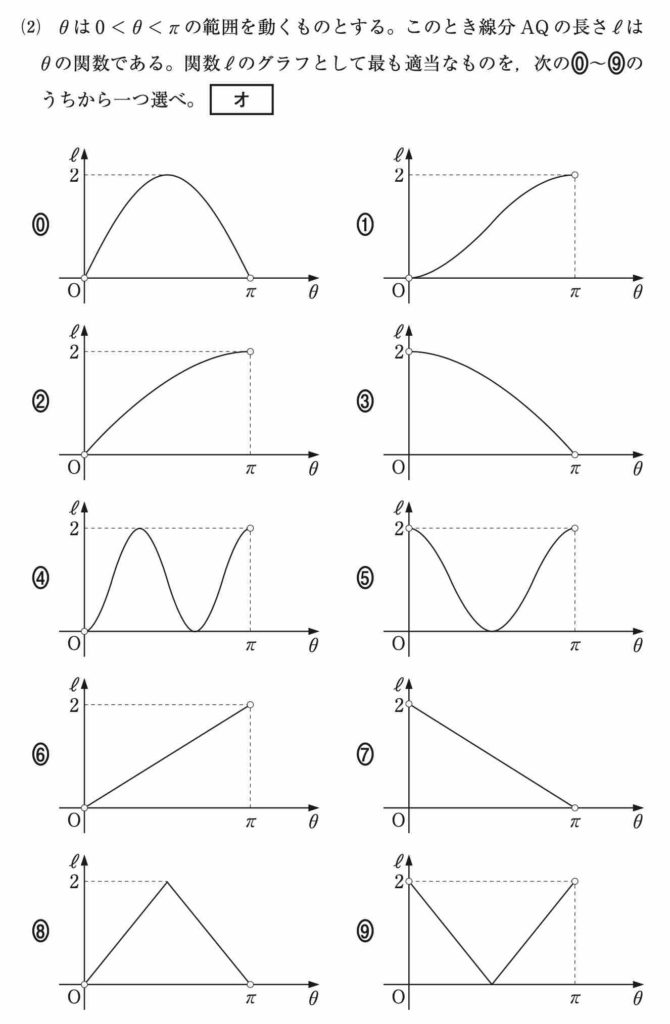
第 1 問〔 1 〕は三角関数からの出題でした。
＜解説＞
(1)
三角比の定義より，点 P の座標は ( cosθ, sinθ ) となります。[ ア ] ① [ イ ] ⓪
∠POQ = 90º であるため Q の x 座標は 
であり，y 座標は 
であるため，点 Q の座標は ( sinθ, -cosθ ) となります。[ ウ ] ⓪ [ エ ] ④
(2)
複数の解法がありますが，ここでは余弦定理を用いてみましょう。
線分 OQ と x 軸の正の部分とのなす角は 
であるため，∠AOQ = 
となります。
△AOQ で余弦定理を用いると 
ですが，2 倍角の公式を用いると 
です。（ 0 < θ < π に注意します。）
これより 
となります。この三角関数の周期は 4π であるため，0 < θ < π の範囲は 4 分の 1 周期に相当します。
・周期が 4π であること
・（範囲外ですが）θ = 0 のとき l = 0 であること
・（範囲外ですが）θ = π のとき l = 2 であること
を踏まえると，正解のグラフは②となります。[ オ ] ②
〔 2 〕は整式の微積分についての問題でした。
＜解説＞
(1)
f(x) が x = -1, 3 で極値をとるため，f'(x) は ( x + 1 )( x - 3 ) で割り切れます。[ キ ] [ ク ]
(2)
定数 a を用いて 
と書けるため，ここから f(x) を計算しましょう。
また曲線 y = f(x) が点 ( 0, 2 ) を通るため，f(x) の定数部分は 2 となることにも注意すると，
と書けます。[ ケ ] - [ セ ]
x = -1 を代入して極値と照らし合わせることで a = -2 がわかり，
が得られますね。
(3)
関数 f(x) は x = -1 で極小値をとり，f(0) = 2 であり，x = 3 で極大値をとります。
したがって方程式 f(x) = 0 の 3 つの実数解のうち負のものは 1 個です。[ ソ ]
関数 f(x) の積分は，y = f(x) のグラフと x 軸で囲まれる領域の符号付き面積です。
a < x < b ではグラフが x 軸の下側にあるので，この範囲での積分結果は -S となります。
b < x < c ではグラフが x 軸の上にあるので，この範囲での積分結果は T となります。
以上より，与えられた積分の結果は - S + T です。[ タ ] ⑦
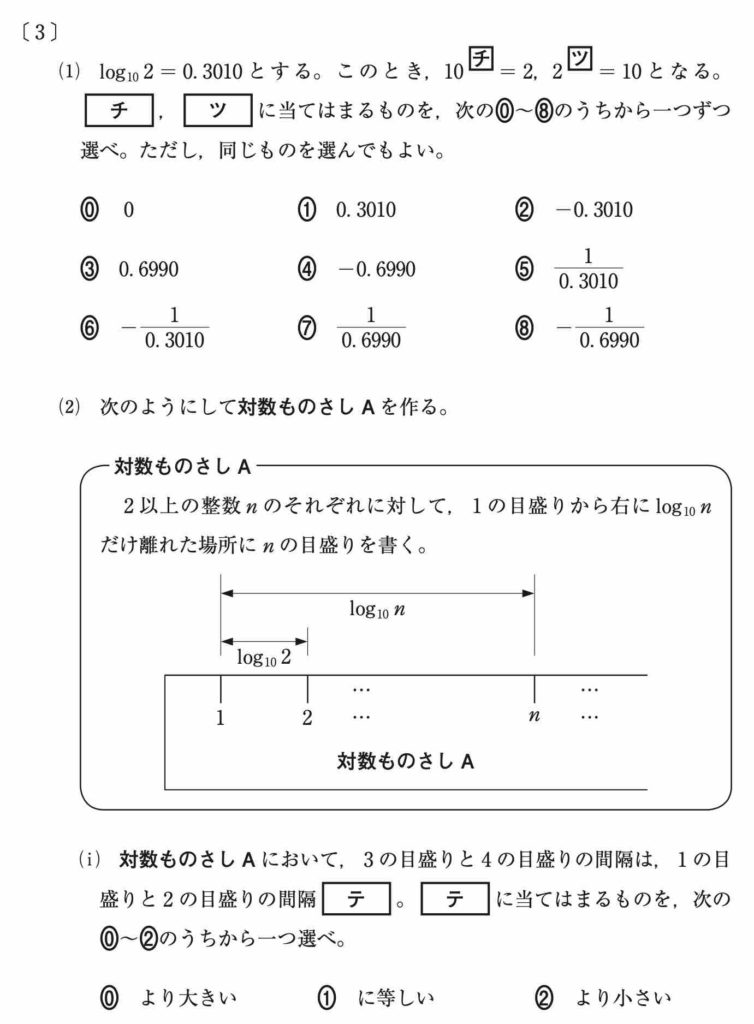
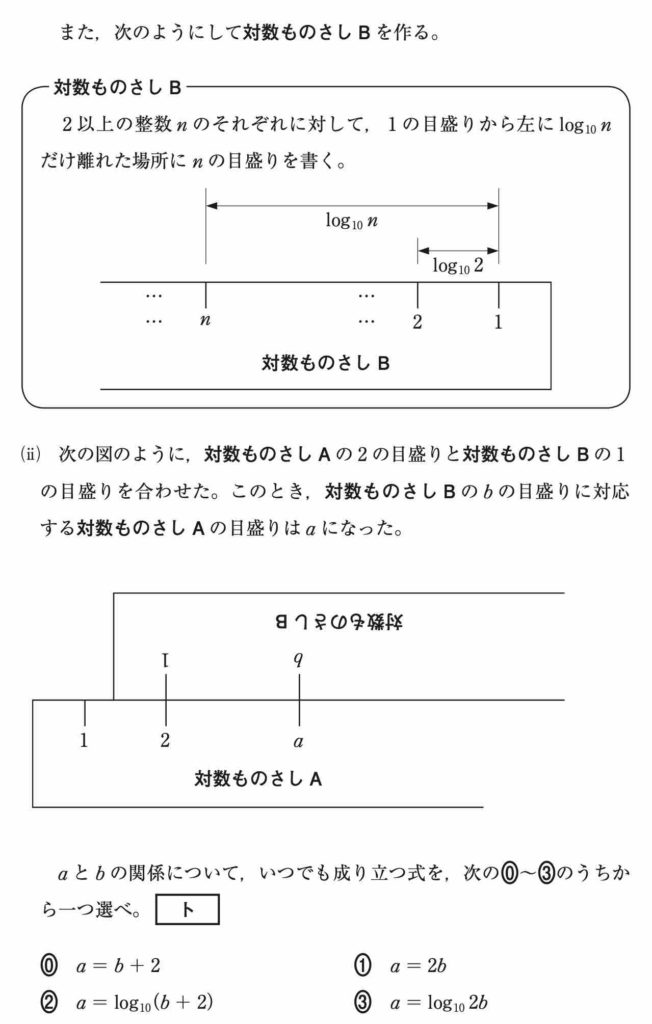
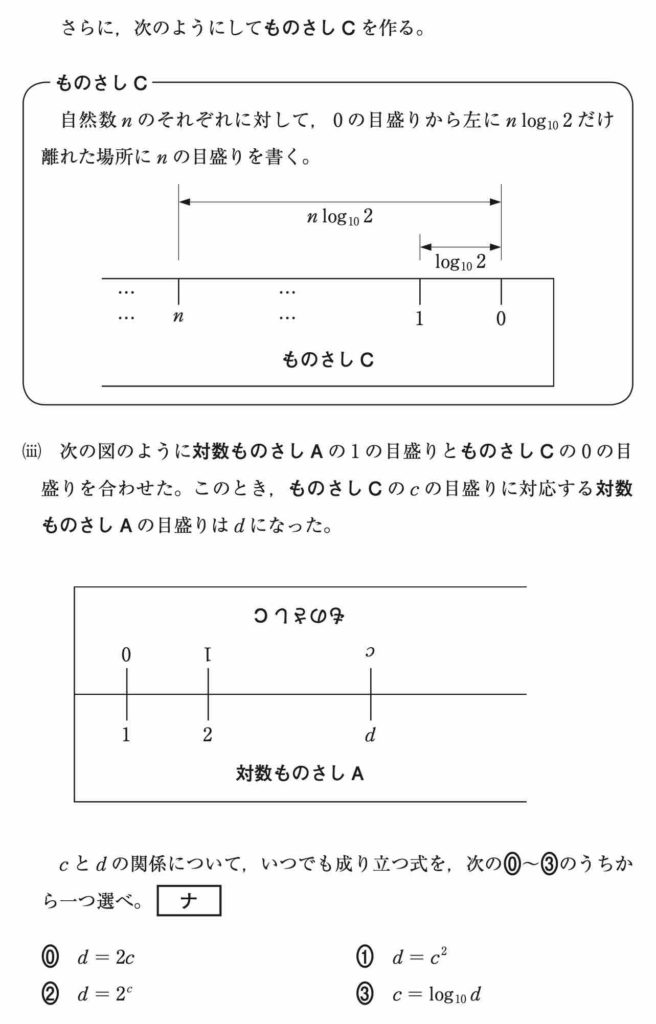
〔 3 〕は指数関数・対数関数からの出題でした。
「ものさし」がたびたび登場するのが印象的ですね。
＜解説＞
(1)
対数の定義より 
であり，いま 
としているので 
が成り立ちます。[ チ ]
また の両辺を 
乗することで 
が成り立ちます。[ ツ ]
(2)
対数ものさしは，いわば「どれくらい差があるか」ではなく「何倍か」を測るものです。
(i)
3 と 4 の比 
は，1 と 2 の比 
よりも小さいため，目盛りの間隔も小さいです。[ テ ]
(ii)
対数ものさしは「比」を測るものであるため，同じ比の 2 目盛りの間隔が等しくなっています。
よって a と b には 
つまり 
の関係が成り立ちます。[ ト ]
(iii)
対数ものさし A では，一定距離進むごとに目盛りの値が一定倍になります。
今回はものさし C （目盛りが一定間隔）の目盛りが 1 進むと A の目盛りが 2 倍になっているため，ものさし C で目盛り c だけ進むと A の目盛りの値は 
倍になります。[ ナ ]
(iv)
これまでのまとめです。
対数ものさしを用いると「掛け算」「割り算」「指数」「対数」の計算はできますが，「足し算」「引き算」などはできませんね。
したがって，実行可能な計算は②③④⑤となります。[ 二 ]
数学IIB 第 2 問 図形と方程式
第 2 問は，いわゆる「図形と方程式」からの出題でした。
あとで五輪マークも出てきます。
〔 1 〕
改めてエネルギーと脂質の量をまとめておきます：
| 1 袋当たり | エネルギー | 脂質 |
| A | 200 kcal | 4 g |
| B | 300 kcal | 2 g |
(1)
(i)
上の表より，エネルギー量についての条件は 
となります。[ ア ]
脂質についての条件は 
ですね。[ イ ]
(ii)
(i) で出した条件を満たしているかどうか，各々チェックしていきます。
答えの個数もわかっているので，解きやすい問題ですね。
⓪と④が正しい選択肢となります。
(iii)
条件①②を図示すると次のようになります。（境界を含む）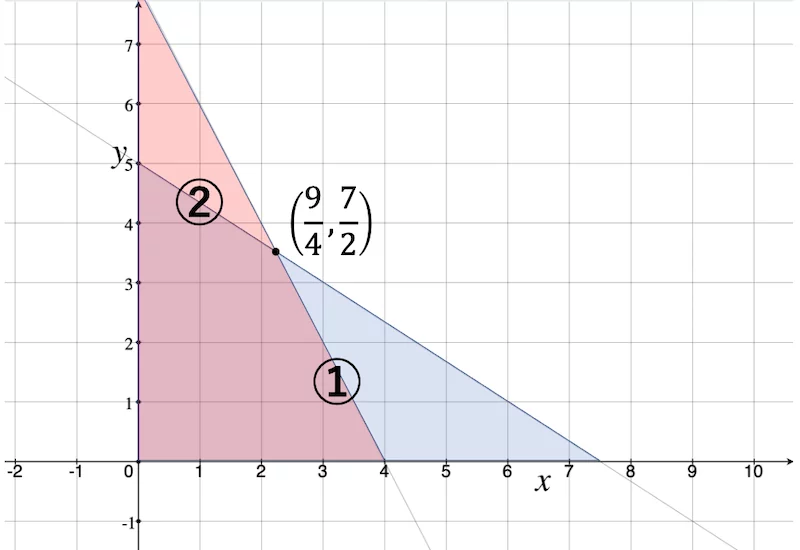
この双方を満たす領域（紫色）において，A と B を食べる袋数の合計 x + y が最大になるような点を考えます。
x + y = k という直線を考え，この領域と共有点を持つような k の最大値を考えれば OK ですね。
点 
[ ク ] - [ サ ] を通るときに k は最大値 
をとります。
したがって食べる量の合計の最大値は 
g となります。[ オ ] - [ キ ]
小分けにできない場合，各袋数は整数に限られます。上の領域でいうと格子点ですね。
格子点のうちA と B を食べる袋数の合計 x + y が最大になるような点は ( 0, 5 ), ( 1, 4 ), ( 2, 3 ), ( 3, 2 ) の 4 つあり [ ソ ] ，このときの食べる量の合計の最大値は 
g です。[ シ ] - [ セ ]
(2)
今度の条件式は 
…③, 
…④となり，図示すると次の通りです。
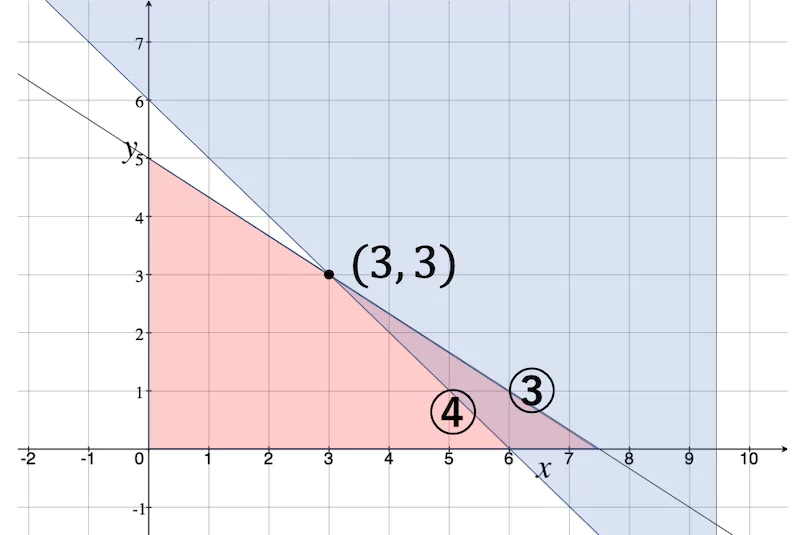
袋を小分けにできない前提で脂質の量を最小にするのが目的です。
上図の紫色の領域と，直線 4x + 2y = k' が共有点をもつような k' の最小値を求めます。
k' が最小になるのは，直線が点 ( 3, 3 ) を通るときで [ タ ] [ チ ]，そのときの脂質量は 18 g です [ ツ ] [ テ ]。
〔 2 〕は軌跡の問題。ある点と放物線上の点の中点の軌跡を求めます。
＜解説＞
(1)
(i)
点 P の座標を 
とすると，線分 AP の中点つまり点 M の座標は 
となります。（ X は任意の実数）
ここから X を消去することで，点 M の軌跡は ① 
となります。[ ト ]
(ii)
x 座標が p だけずれると，AP の中点である点 M の x 座標は 
だけずれることになります。[ ナ ]
(iii)
点 A の座標が ( p, q ) であるときの軌跡の方程式を立て，真面目に 
と連立するのもよいですが，そこまで真剣に考えずとも答えを出せます。
(i) (ii) で「点 M の方程式において，
の係数は 2 である」ということがわかっています。
あとは放物線の頂点をいろいろずらして，放物線 との交点を考えれば OK です。
答えは①④⑤となります。[ ニ ]
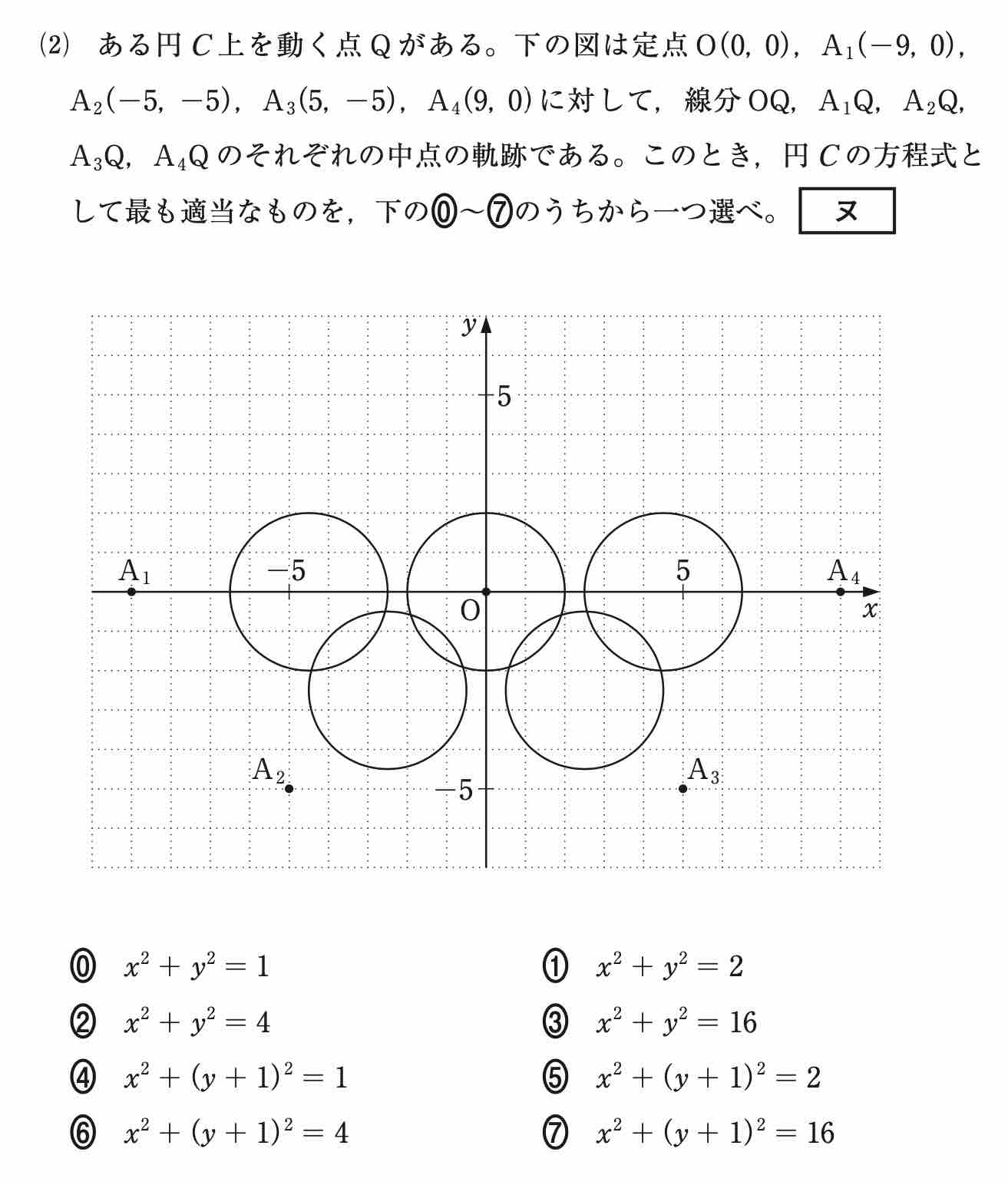
共通テストの初回は東京オリンピックのすぐ後の予定だったので，五輪マークに関する問題が出題されています。
(2)
図形全体が左右対称になっているので，円 C は y 軸対称の位置にあると断定して OK です。
円 C 上の点と原点の中点の奇跡が円 
であることから，円 C はこの円を原点中心に 2 倍拡大したものであり，答えは③ 
となります。[ ヌ ]
あとは選択肢③を仮定したときの奇跡が，上図のように五輪になるか確認しておけば問題ありません。（論理的に順当な解き方ではありませんが，限られた時間の中で効率的に問題を解くにはこれくらいがよいでしょう。）
数学IIB 第 3 問 統計
第 3 問は統計からの出題でした。
これまで行われていたセンター試験とは問題の順序が異なるのが印象的ですね。
＜解説＞
(1)
シンプルな二項分布の問題です。
全く読書をしない学生の母比率が 50% であるため，P 大学生の標本 400 人のうち全く読書をしない学生の人数の期待値は 400 人 x 0.5 = 200 人 となります。[ ア ] - [ ウ ]
また標本の大きさ 400 は十分に大きいので，この二項分布は正規分布に近くなります。平均は元の母比率 50% より 0.5 で [ エ ]，標準偏差は 
と計算できます。[ オ ] - [ キ ]
人数の分布ではなく比率の分布であることに注意しましょう。
(2)
昨年度の全国調査との比較をします。
(i)
標本平均の分布の平均は，母平均と等しく，それは仮定より 24 分です。[ ク ] [ ケ ]
標本平均の標準偏差は 
となるのでした。分母の 
がポイントですね。[ コ ] [ サ ]
(ii)
であるとき，標本平均の分布は平均 24，標準偏差 
となります。
標本平均が 30 分以上となる確率を求めるには，正規分布表を使えば OK ですね。
30 分というのは 3σ に相当し，正規分布の値が 3 以上になる確率は 1 - ( 0.5 + 0.4987 ) = 0.0013 です。[ シ ] - [ ソ ]
最後の選択肢は，1 つ 1 つ順番に検討していくほかありません。
ただ，P 大学の全学生の読書時間の平均については，全学生の人数が不明な以上，標準偏差を求めることができません。
その意味で②③は解答から外れることになります。
今回の確率は 0.1587 であるため，人数が少なくなりそうな①④が候補ですが，無作為抽出した 1 人の学生については標準偏差が 40 なので，そう簡単に確率が 0.15 程度まで小さくなることはなさそうです。
以上の考察より答えが④であると予想でき，あとは正規分布表を見て答え合わせをすれば OK です。[ タ ]
実際，標準正規分布の値が 1 以上となる確率は 1 - ( 0.5 + 0.3413 ) = 0.1587 となっていますね。
(3)
(i)
標本の大きさ 400 は十分に大きいので，正規分布の信頼区間を利用できます。
大きさ 400 の標本平均の分布の標準偏差は であったため，信頼区間の端 A は 
です。[ チ ]
(ii)
「95% の信頼区間」は，「母平均が 95% の確率でその範囲に入る」という意味です。
これに該当する選択肢は④となります。[ ツ ]
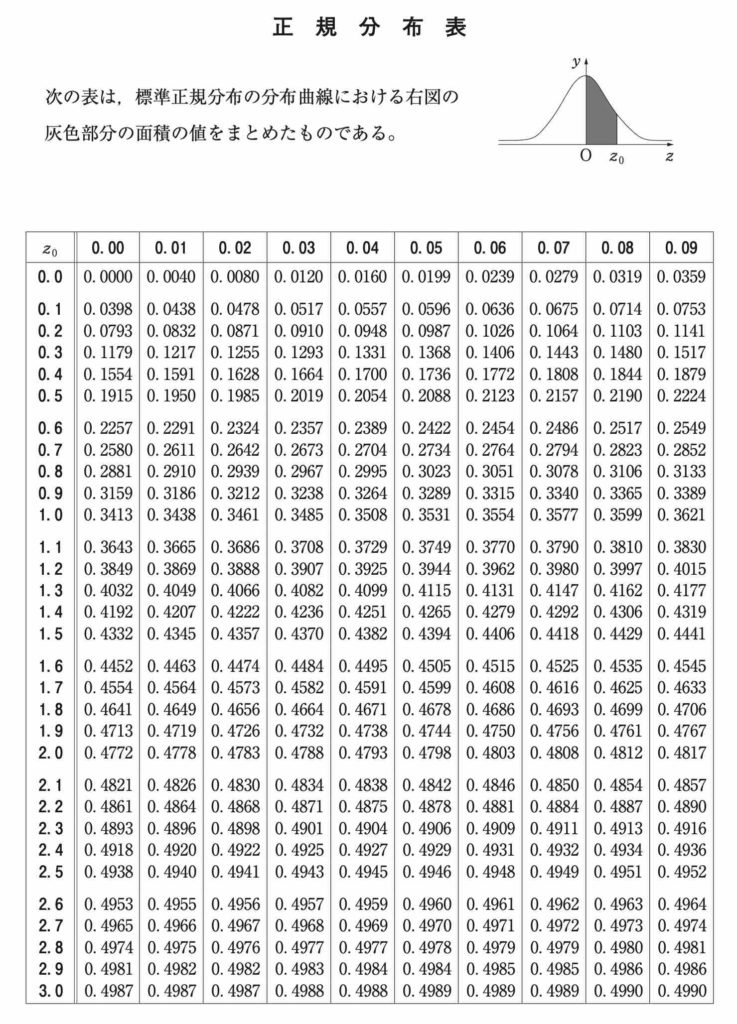
正規分布表は，今回の問題を解く上で複数回用いました。
これがないと（実質的に）解けない問題があるので，表の存在を忘れないようにしましょう。
数学IIB 第 4 問
(1) はシンプルな漸化式の問題。
特性方程式を解くのは，等比数列の形に変形するためでした。その目的を理解できる問題です。
＜解説＞
(1)
(i)
と 
の定数部分を比較すると -8 = -2k となり，これより k = 4 が得られます。[ ア ]
(ii)
k = 4 よりこの漸化式は 
と変形でき，数列 
は公比 3 の等比数列となります。
よりその数列の初項は 6 - 4 = 2 なので，
つまり 
です。[ イ ] - [ エ ]
(2) では漸化式に n が入っており，難易度が上がっています。
まず n を消去し，その漸化式を (1) 同様に解くという流れです。
＜解説＞
(i)
漸化式より 
であるため，
です。[ オ ]
(ii)
, 
の 2 式を引き算することで 
つまり 
が得られます。
厄介だった n が，引き算をすることで（定数を除いて）消えます。
(iii)
という漸化式を等比数列の形に直すのですが，ここで伏線回収があります。
この p に関する漸化式は，(1) で解いたものと（初項も含めて）全く同じです。
よって漸化式を解く必要はなく，
が得られます。
(3) では，問題 B の数列を別の方法で解こうとしています。
この方法のポイントは（ n + 1 だけの式）＝（ n だけの式）という形にすることです。
＜解説＞
(i)
左辺には n + 1 だけ，右辺には n だけを登場させる必要があるので，[ サ ] = ③，[ シ ] = ⓪ となります。
(ii)
という漸化式と が一致するように s, t を調整します。
を整理すると 
なので，係数比較をすることで 
となり，これを解くことで s = -4, t = 1 が得られます。[ ス ] - [ ソ ]
(4) (5) はこれまでのまとめです。特に (5) は手間がかかりますが，明らかに差がつく問題です。
また解法も与えられているので，それにのっとって根気よく計算していきます。
(4)
(3) の結果を用いると，数列 {
} は公比 3 の等比数列です。
初項は 
であるため 
であるため，
が得られます。[ タ ] - [ ツ ]
(5)
実践的には難問です。
n の二次式があるので，漸化式 
を 
という形に変形することを目標にします。
式を展開して係数比較することで 
を得るので，これを解き 
を得ます。
したがって数列 {
} は公比 3 の等比数列です。
初項は 
なので 
となり，これより 
がしたがいます。[ テ ] - [ ヌ ]
数学IIB 第 5 問 ベクトル
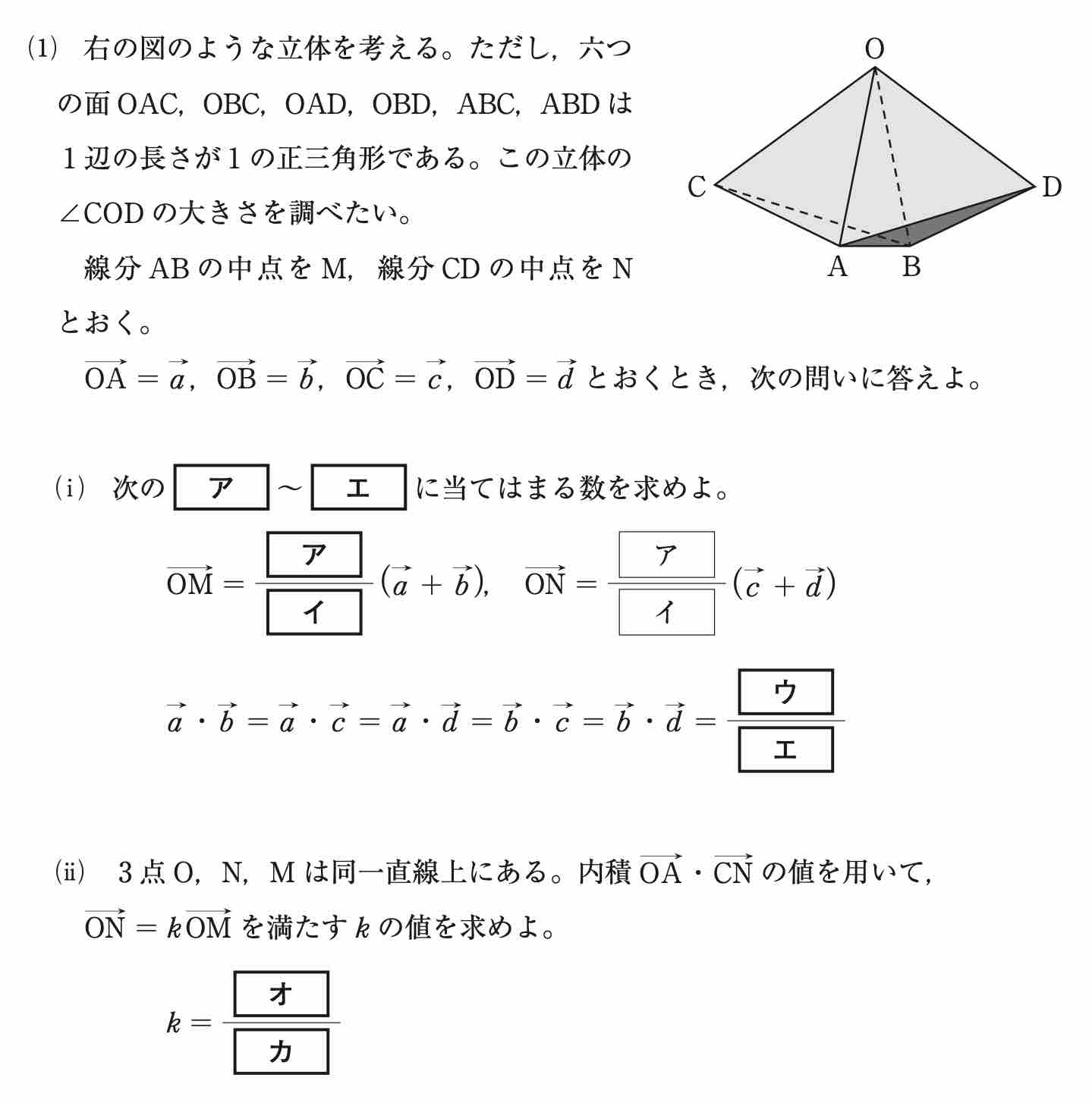
(1) は正三角形のみからなる立体に関する問題でした。
誘導をよく読み，問題を解いていきましょう。
＜解説＞
(1)
(i)
M は線分 AB の中点であるため 
であり，N は線分 CD の中点であるため 
です。[ ア ] [ イ ]
またこの立体を構成する平面は全て正三角形であるため，
です。[ ウ ] [ エ ]
(ii)
対称性より線分 OA と線分 CN は垂直になっています。
であるため 
より確かに内積が 0 になっていますね。
一方で 
とおくと 
なので，
と書けます。
したがって
であり，(i) の結果を用いると 
となります。
これが 0 であればよいので 
であることがわかります。[ オ ] [ カ ]
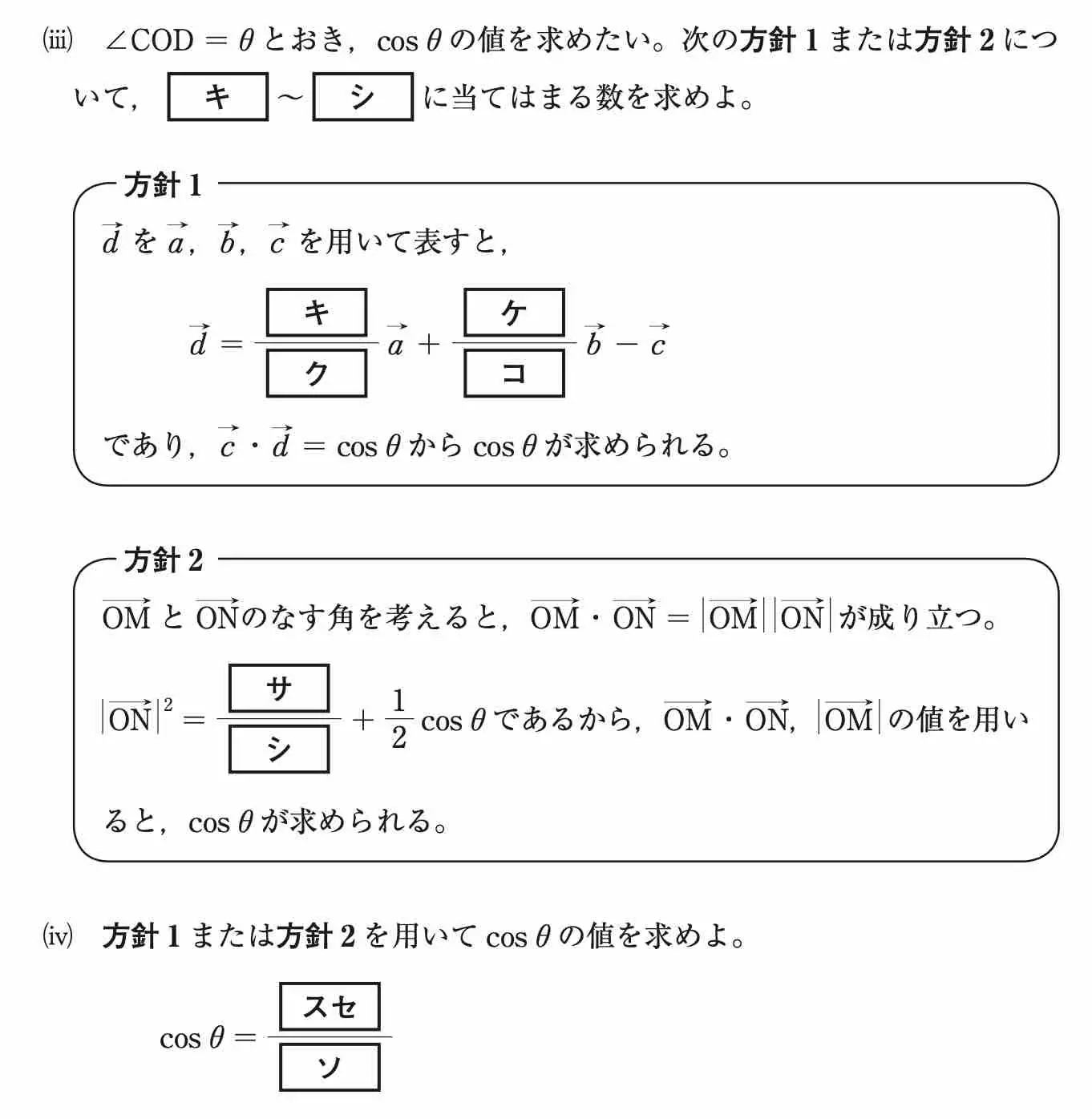
これまでの結果を用いて，∠COD の余弦を求めていきます。
(iii)
(ii) の結果より 
であるため 
が成り立ち，これより 
を得ます。[ キ ] - [ コ ]
なので 
が成り立ちます。[ サ ] [ シ ]
(iv)
例えば 方針1 を用いてみましょう。
なので 
となります。
一方，方針1 にある通り 
であるため，2 式より 
を得ます。[ ス ] - [ ソ ]
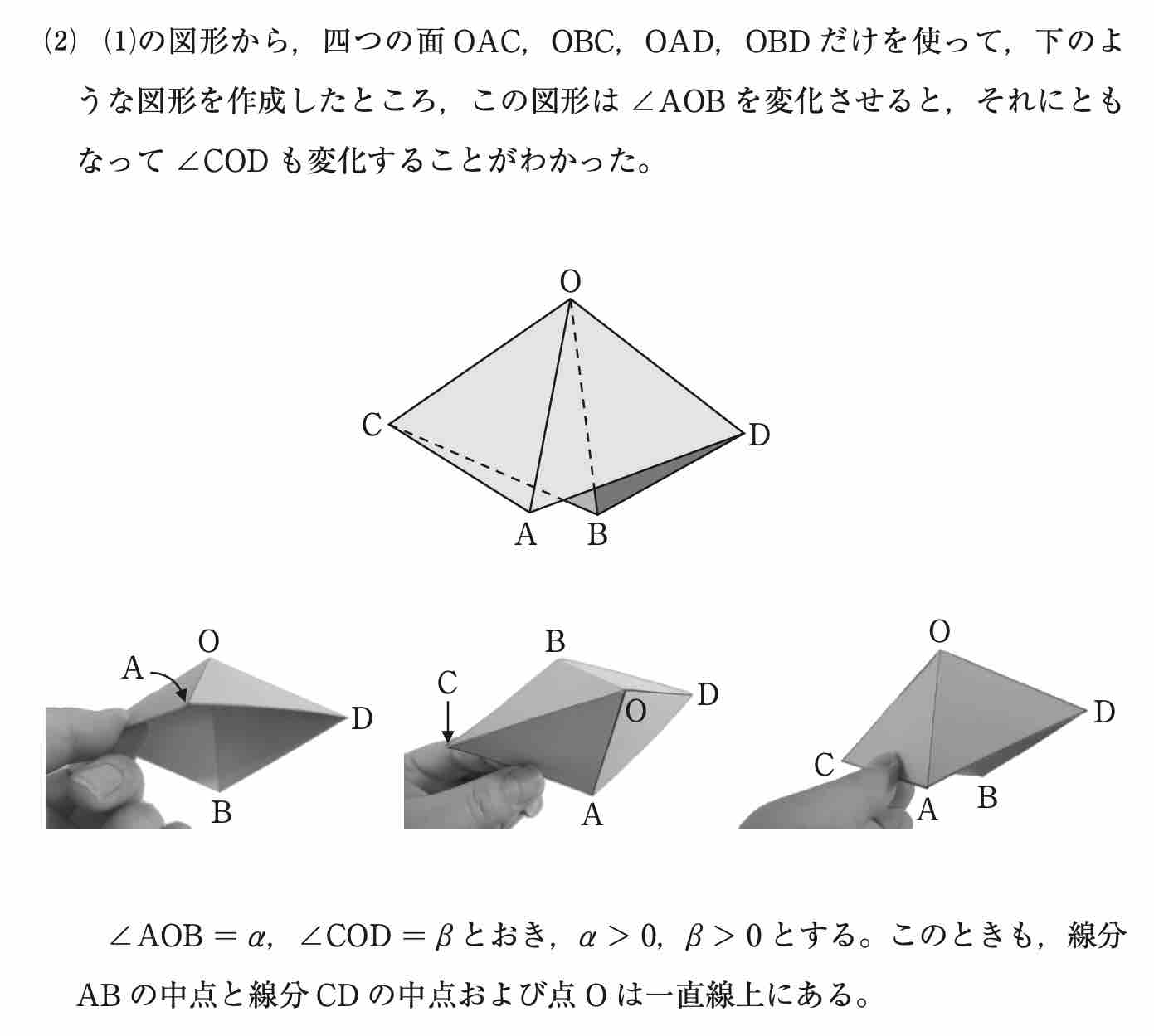
(2) では，(1) の条件のうちいくつかが使えなくなっている（状況が変化している）ことに注意しましょう。
＜解説＞
(i)
先ほどと同じベクトルの記号を用いることにします。
∠AOB = α より 
であり，
が成り立ちます。
また 方針2 より 
となります。
(1) (ii) と同じ方法で 
となる実数 k' を求めます。
なのは同じですが，
, 
である点が先ほどと違いますね。
から k' を求めると 
となります。
また 
であるため，
とわかります。
一方で 
, 
, 
であるため，これらより 
が成り立ちます。[ タ ]
(ii)
α = β のとき，(i) の結果も合わせると 
つまり 
が成り立ちます。
これより α = 90º とわかります。[ チ ] [ ツ ]
またこのとき k' = 1 であり，
より 
つまり 
が成り立ちます。
の係数の和が 1 なので，点 D は平面 ABC 上にあることになります。[ テ ] = ①
まとめ
平成 30 年度実施の，共通テスト試行調査（プレテスト）数学IIB の解説でした。
これまでのセンター試験と比較すると，
・会話文を用いた問題が出題されている。
・図表が多く用いられている。
・計算量が大きく減少している。
といった特徴があります。
会話・問題文を注意深く読み，誘導にうまく乗るのが高得点獲得のポイント。
数字（数式）にばかり着目せず，会話文を最初から読むなど，焦らず解いていきましょう。
とはいえ，共通テストの問題の演習は数学 IIB の学習が終わった後でよいでしょう。
教科書レベルの内容に抜けがあるうちは，地道な勉強を忘れずに！
共通テストに関連する情報は，例えば下記のページにまとめられています。
必要に応じて参照してください。
