スタクラ情報局
2019.11.27
センター試験【数学】の問題構成や攻略法を伝授!
センター試験 数学の問題構成と攻略法
今回は、センター試験数学(数学①、数学②)の問題構成および攻略法について説明していきます。
※センター試験での科目名と内容の対応は以下の通りです:
数学①:数学 I または 数学 I + A
数学②:数学 II または 数学 II + B
本記事では、受験者数が比較的多い「数学 I + A」および「数学 II + B」を対象とします。
試験時間・配点
センター試験各科目の試験時間や配点は以下の通りです:
科目 | 試験時間 | 配点 |
英語(筆記) | 80分 | 200点 |
英語(リスニング) | 60分 | 50点 |
数学① | 60分 | 100点 |
数学② | 60分 | 100点 |
国語(現・古・漢) | 80分 | 200点 |
理科① | 60分 | 100点 |
理科② | 1科目 60分 | 1科目 100点 |
地理歴史 公民 | 1科目 60分 | 1科目 100点 |
数学は合計で200点となっています。
数学①(数学 I + A)
数学 I + A は必答問題と選択問題により構成されます。
例年の構成は以下の通りです:
問題 | 分野 | 配点 | 選択方法 |
第 1 問 | 数と式、論理と証明、二次関数 | 30点 | 必答 |
第 2 問 | 図形と計量、データの分析 | 30点 | 必答 |
第 3 問 | 場合の数・確率 | 20点 | いずれか 2 問を |
第 4 問 | 整数 | 20点 | |
第 5 問 | 図形と計量・図形の性質 | 20点 |
選択問題も含めて考えると、全ての分野から満遍なく出題されます。
他科目でもそうですが、センター試験は「浅く、広く」というタイプの試験なので、ヤマをはって凌ぐことができません。
数学②(数学 II + B)
数学 II + B も必答問題と選択問題により構成されます。
例年の構成は以下の通りです:
問題 | 分野 | 配点 | 選択方法 |
第 1 問 | 三角関数、指数・対数関数 | 30点 | 必答 |
第 2 問 | 微分・積分 | 30点 | 必答 |
第 3 問 | 数列 | 20点 | いずれか 2 問を選択し、解答 |
第 4 問 | ベクトル | 20点 | |
第 5 問 | 統計 | 20点 |
やはり、全ての分野から満遍なく出題されます。
先述の通り制限時間は 60 分なのですが、これが結構キツいですね。
センター数学①(I + A)の攻略法
では次に、センター数学で高得点を獲得する方法をご紹介します。
問題例は、全て2019年センター試験(本試験)のものです。
第 1 問 [1] 数と式

式の値、因数分解、絶対値などのシンプルな計算がテーマの大問です。
計算量は多くなく、難易度も高くありません。
こうした問題は、なるべく苦労がない方法で解くのが大切です。
例えば上の問題の最初の因数分解を見てみましょう。
[ア] と [イ] の両方を文字でおいて展開し、係数比較をすると計算量が多くなります。
でも、次のように解くとどうでしょうか。
定数項をみると、[ア] の 2 乗が 9 になるらしい。
[ア] は 1 桁の整数だ。
だから [ア] は 3 とわかる。
定数項をみると、[イ] の 2 乗が 1 になるらしい。
[イ] は 1 桁の整数だ。
だから [イ] は 1 とわかる。
これは、全て暗算でできるはずです。
[ア] = p, [イ] = q などとおいてしまうよりはずっと楽です。
慣れている人は 5 秒くらいで、数学が苦手でも 30 秒あれば解けることでしょう。
こうした小さな工夫の積み重ねで、センター数学本番も有利になります。
第 1 問 [2] 論理と証明

「命題」についての大問です。
この問題に限らず、命題というものへの理解は数学で大変重要です。

上のように、必要条件・十分条件に関する問題が毎年必ず出題されています。
p → q が成り立つときに、p は q であるための十分条件という。
p → q が成り立つときに、q は p であるための必要条件という。
これらの定義は何があっても覚えておきましょう。
あとは必要条件・十分条件の定義を元に、各命題の真偽を検証するだけです。
第 1 問 [3] 二次関数

数学 I で最もしんどい分野ともいえる二次関数。
平方完成してグラフの頂点の座標を求めるという作業は毎年のように必要となります。
また、グラフの移動(各軸に平行に移動する)も頻出。
これらは絶対に覚えておきましょう。
[1] [2] と比べると計算量が多い傾向にあるので、計算ミスに要注意です。
第 2 問 [1] 図形と計量
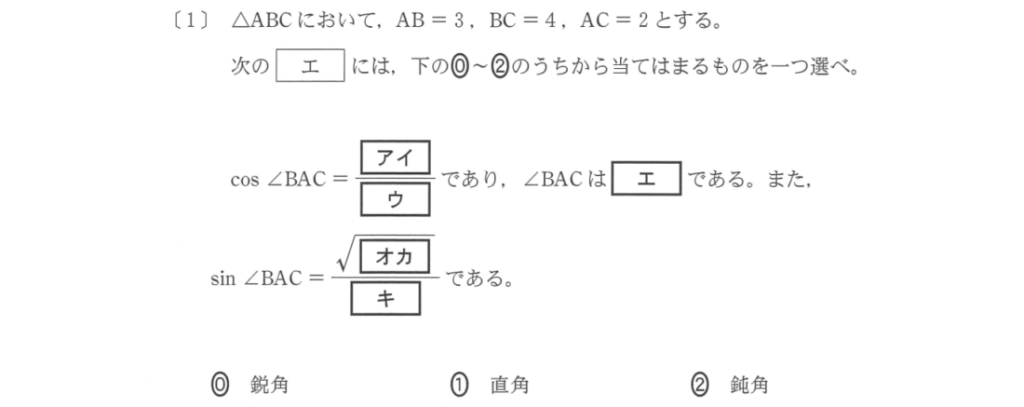
三角比に関する問題が出題されます。
以下のような計算が頻出なので、練習しておきましょう:
三角形で三辺の長さが与えられたときに、ある角度の余弦を計算する。
三角形で辺の長さや角度が与えられたときに、その三角形の外接円の半径を計算する。
正弦(sin)や余弦(cos)の値から、具体的な角度を求める。
三角形の形状等にはバリエーションはあるものの、問題の構造自体は数パターンしかありません。
問題演習で経験をつめば、初見の問題に出くわしてビックリすることもなくなります。
第 2 問 [2] データの分析

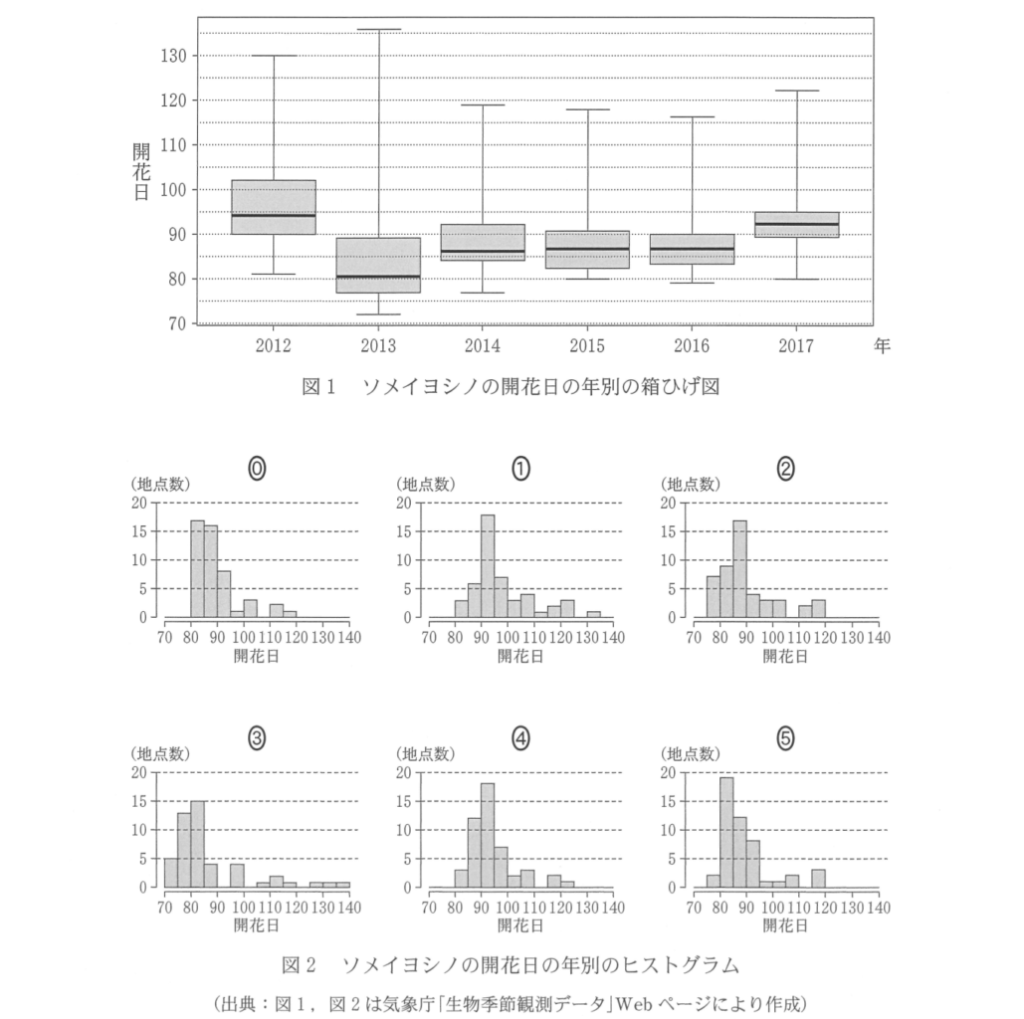
統計の基礎的な内容を問うものです。
上の問題では箱ひげ図とヒストグラムの対応が出題されていますが、このように「データと図の行き来」「図どうしの行き来」を問う問題が多いです。
グラフを読み取り、「こういう特徴を持ったデータ群なんだな」と想像する力が求められます。
そのためには、まず平均や分散、四分位などの定義をきっちり学ぶ必要があるのです。
問題演習に入る前に、教科書の読み直しをするのが大切です。
第 3 問 場合の数・確率
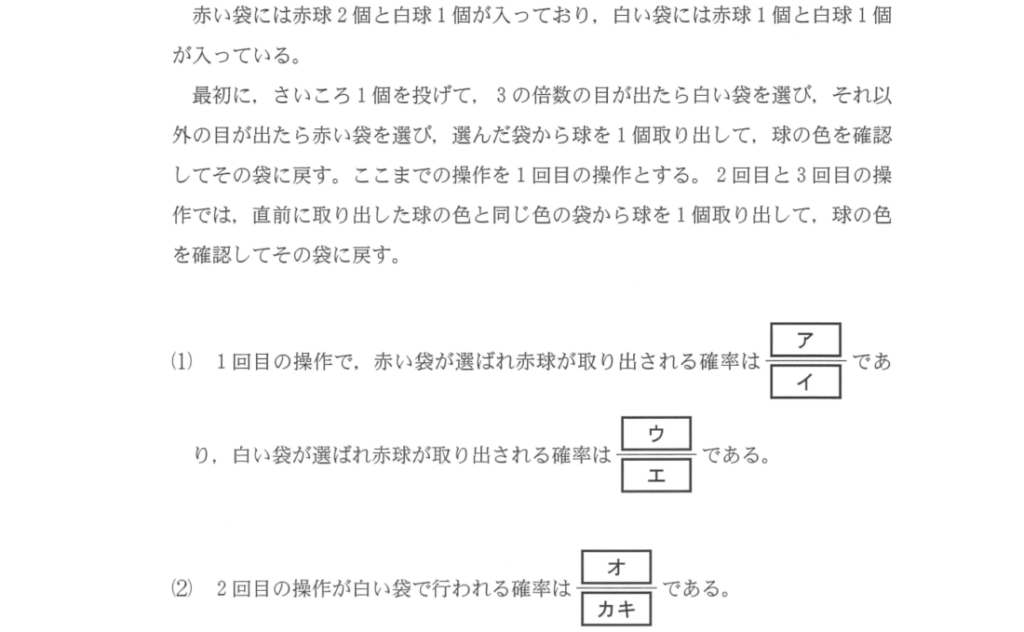
場合の数や確率の計算をします。
さいころを振る、袋から玉を出すなど、問題集に頻出の題材となっています。
奇を衒った問題は登場しないので安心してください。
この分野のポイントは以下の通りです:
場合の数は、「漏れなく重複なく」
確率は「同様に確からしい」事象をベースに計算
条件付き確率の定義を知っておこう
どれも大変重要です。日頃の問題演習でも、これらを意識しましょう。
第 4 問 整数

不定方程式や倍数・約数の話題を扱います。
特に出題されやすいのは
約数・倍数に関する知識(約数の和の計算など)
互助法や、それを利用した不定方程式の解法
あたりですね。
この大問も、バリエーションが豊富なわけではありません。
教科書傍用問題集やチャート式などで、類似の問題を解きまくりましょう。
第 5 問 図形と計量・図形の性質
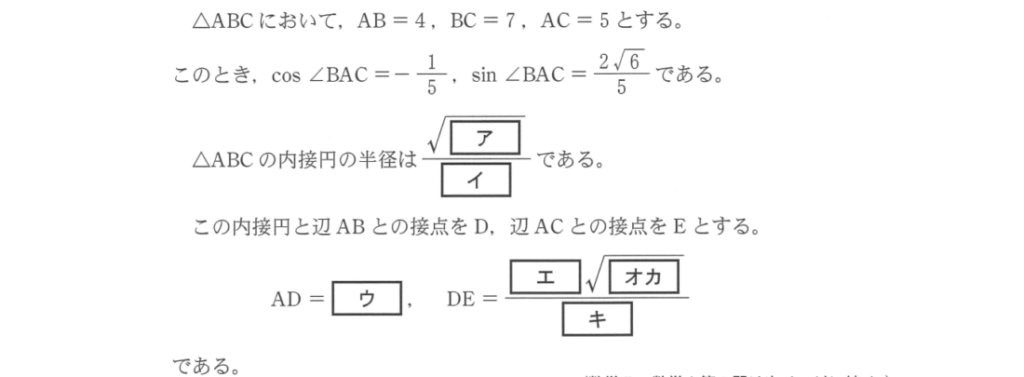
メネラウスの定理やチェバの定理、角の二等分線の性質などを扱います。
三角比とも融合しているケースがほとんどです。
図形に関する総合問題といえるでしょう。
この大問のポイントは、「図をある程度丁寧に描く」ということです。
センター試験の図形問題には図が用意されていません。
したがって、自分でこしらえる必要があるのです。
完璧な図は当然描けませんが、あまりに雑だと
等しくない辺が等しく見えてしまう
平行でない辺が平行に見えてしまう
点や直線の位置関係を見誤ってしまう
…
などの事態が起こり、自分を混乱させてしまうのです。
日頃の問題演習から、ノートに図を書く習慣をつけましょう。
センター数学①(II + B)の攻略法
第 1 問 [1] 三角関数
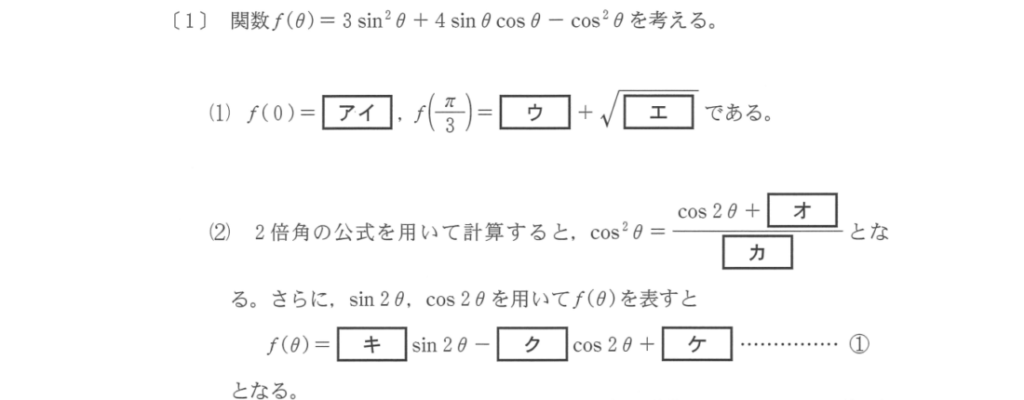
三角関数についての問題です。
次のような問題がよく出題されます。
三角関数を合成し、一つの三角比で表現し、値域を求める
三角関数を文字でおき、二次関数として値域を求める
三角関数の合成を自身で計算するのは、不慣れな人にとって難しいことでしょう。
なぜ・どのようにして合成できるのか、教科書等でよく復習してください。
第 1 問 [2] 指数・対数関数

指数関数や対数関数について出題され、上のように融合されることもあります。
大抵は指数や対数を用いた方程式の話題です。
こうした方程式は、形式や解法が数パターンしかありません。
対数の和を積に直したり、指数全体を文字で置いたりして、二次方程式に変形するのがほとんどです。
そうした問題に習熟していれば [2] も問題なく正解できるでしょう。
ただし、連立方程式レベルになると教科書には問題がない可能性があるので、チャート式などの参考書で別途演習する必要があります。
第 2 問 微分・積分

極値や接線の傾き、それに面積という形で微分・積分を総合的に用いる大問です。
変わった問題は一切登場しないので、解き方で悩むことはないでしょう。
一方、微分や積分の計算は、本質的に計算量が多くなりがちです。
文字・分数を含んだ計算も頻繁に登場するので、計算のスピードを上げつつ計算ミスを防ぐのがキモです。
たくさん問題演習をするのが命。
計算を大量にこなすことで、計算を簡略に・ミスなく進めるコツがわかってくるでしょう。
第 3 問 数列
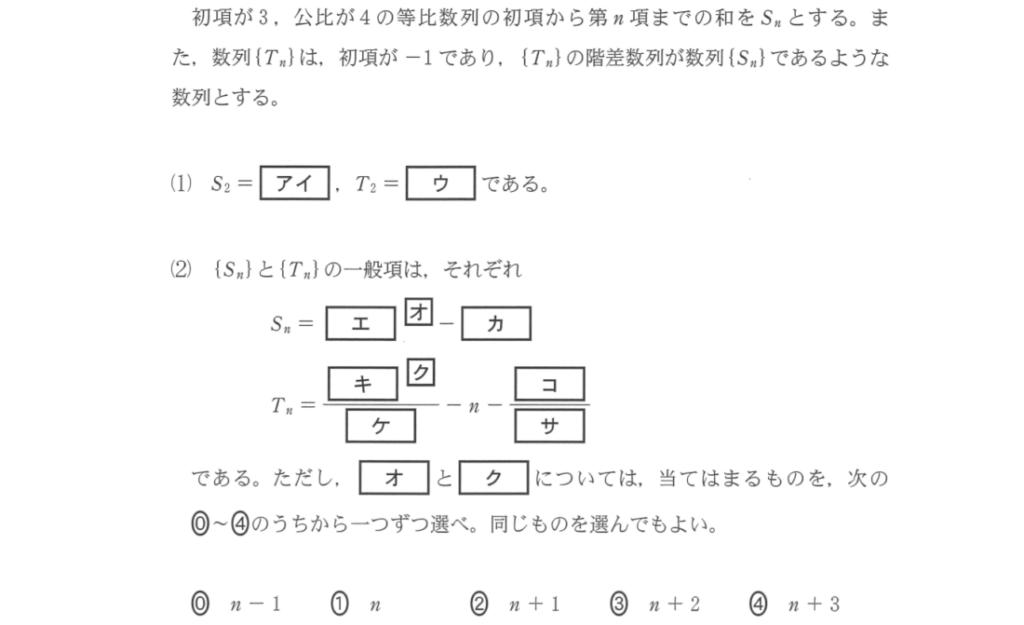
数列の一般項や和を計算する問題です。
等比数列になると、指数が登場することもあり計算が複雑になります。
ミスが最も発生しやすい大問といえるでしょう。
重要なのは、出てきた結果が正しいかどうか確認することです。
例えば上の問題の場合、S_n および T_n が求まったら、n = 1, 2 あたりの簡単な数で検証してみます。
正しく求められているかどうか、ある程度の精度でチェックできるでしょう。
結果が出たら、いくつかの n で検算をしてから次に進む。
面倒なようでもコレが一番効率的です。
第 4 問 ベクトル
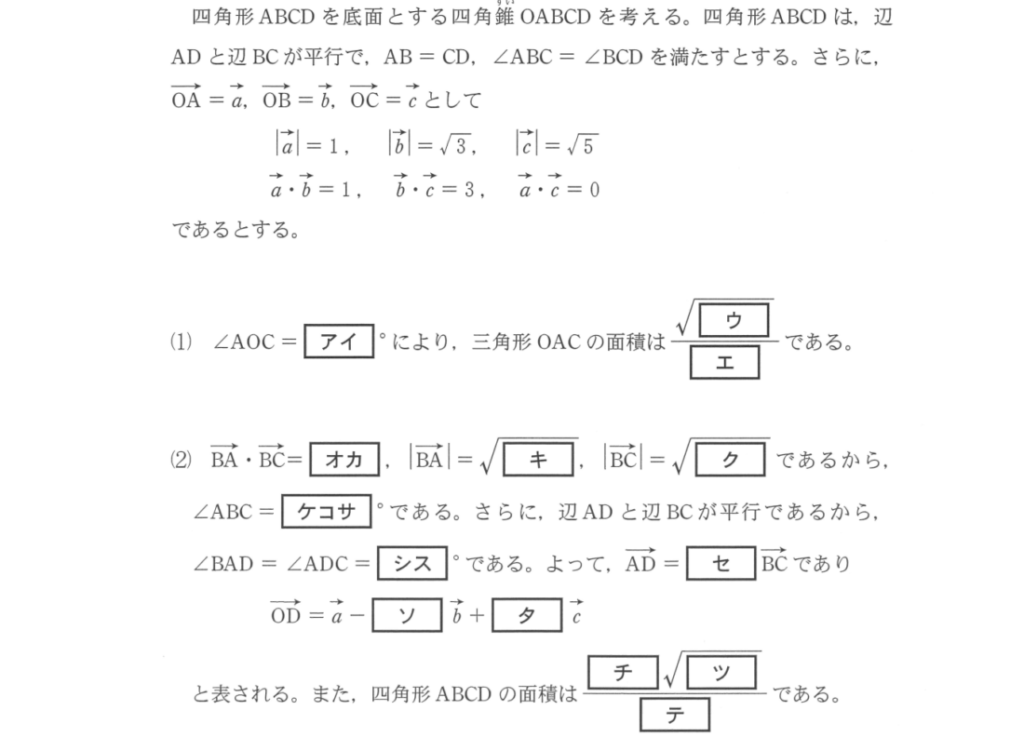
ベクトルに関する総合的な問題が出題されます。
といっても、できるべき計算の種類は限られているのです。
ベクトルの絶対値の計算
複数のベクトルのなす角の計算
三角形の面積の計算
内分点等の表現
この辺りをしっかり学習しておけば、知識面で苦労することはありません。
多くの場合空間図形が題材なので、平面図形だけで妥協せずに空間図形も対策をしておきましょう。
第 5 問 統計

数学 B の教科書の最後に載っている統計分野の問題です。
多くの受験生は第 3 問および第 4 問を解くと思いますが、これを選択することも可能です。
とはいえ他の大問と同レベルですので、学校等でしっかり学習した人のみ選択しましょう。
正規分布の度数分布表も用いつつ計算を進めますが、問題のバリエーションは 5 問の中で最も少ないです。
期待値や分散、標準偏差の定義
それらを用いた計算
正規分布や二項分布などの代表的な分布についての知識
を身に付けましょう。
選択問題の選び方
数学①、数学②ともに選択問題があります。
センター試験では大問による難易度の差が大きくならないよう調整されているので、難易度を軸に選ぶのは避けましょう。
パッと見での難易度と解き進めたときの難易度は違うためです。
学校や塾で勉強したことがある
過去の成績を見るに得意である
演習量が多い
計算ミスをしない自信がある
といった基準で選ぶのが大切です。
問題を眺めて比較検討する時間が惜しい場合は、最初から選択する問題を決めてしまうのもアリです。
まとめ
センター数学(数学①、数学②)について、問題構成や攻略法を紹介しました。
2020年のセンター試験まであとわずか。
この記事を何度も読み返して、センター数学で高得点をとるコツを頭に叩き込んでください。
過去問演習をするときも、以上の内容を意識しましょう!
