スタクラ情報局

1. 三角比の頻出問題を総ざらい！

学年末試験が近づいてきました。

この記事では、三角比関連の頻出問題、特に方程式・不等式あたりをご紹介していきます。

試験対策として、ここで説明した問題はぜひ解けるようにしておきましょう！

前提知識

まずは、問題を解くにあたり必要な知識を振り返りましょう。

相互関係

三角比には、次のような相互関係があるのでした。

三角比の定義と合わせて、覚えておきましょう。

正弦定理・余弦定理

これら二つの定理も、種々の問題を解く上では必須です。

以下、△ABC において AB = c, BC = a, CA = b, ∠ABC = B, ∠BCA = C, ∠CAB = A とします。

＜正弦定理＞

＜余弦定理＞

では、具体的に頻出問題を見ていきましょう！

必ず抑えたい三角比の値

どういう問題を解くにしても、簡単な角度の三角比の値は覚えておかなくてはなりません。

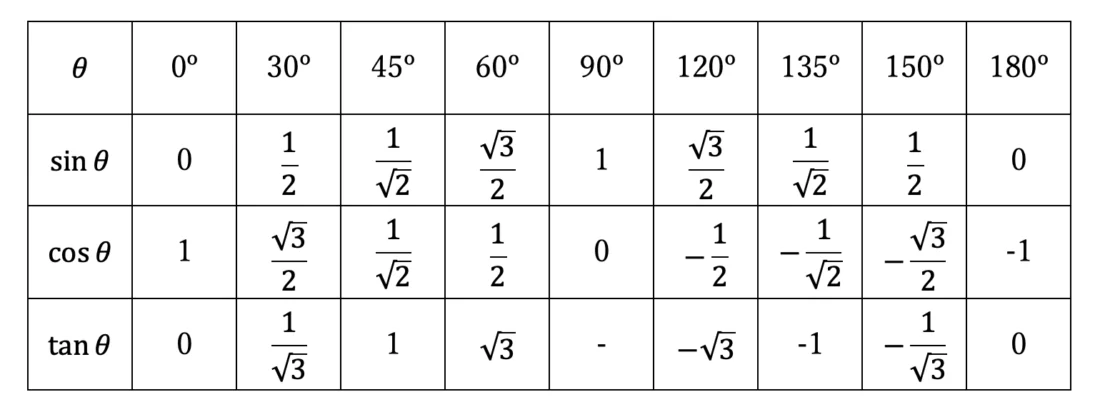
何も見ずに、そして迷わずにこの表を埋められる必要があります。

まだ値があやふやな人は、百マス計算のようにガンガン練習しておきましょう！

相互関係を用いた問題（鋭角）

問題

A は鋭角とする。 のとき、 の値を求めよ。

方針

三角比の相互関係を用いて、余弦や正接の値を計算していきます。
A が鋭角であることに注意して、正しい符号を選択します。

解答

 であるため、

A は鋭角であり cosA > 0 であるため、

また、これより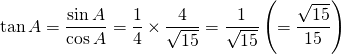

相互関係を用いた問題（鈍角）

問題

とする。tanB = -3 のとき、sinB, cosB の値を求めよ。

方針

基本方針は変わりませんが、符号の選択に注意が必要です。

解答

であり、tanB < 0 より B は鈍角であるため cosB < 0 となる。

したがって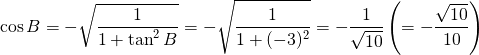

また となる。

「簡単にする」問題１

問題

tan(180º - A)tan(90º - A) を簡単にせよ。

方針

180º - A, 90º - A の三角比を簡単にしてから計算を実行します。

解答

,  であるため、

「簡単にする」問題２

問題

- cos(90º + θ) - cosθ + sin(90º + θ) - cos(90º - θ) の値を求めよ。ただし  とする。

方針

90º - θ や 90º + θ に着目して、式を変形していきます。

「値を求めよ」という問題の場合は、答えに三角比が含まれないシンプルな値になると思って差し支えありません。

解答

cos(90º + θ) = - sinθ, sin(90º + θ) = cosθ, cos(90º - θ) = sinθ であるため

- cos(90º + θ) - cosθ + sin(90º + θ) - cos(90º - θ) = sinθ - cosθ + cosθ - sinθ = 0

三角比を用いた方程式の問題１

のとき、次の等式を満たす θ を求めよ。

(1)

(2)

方針

三角比は、座標平面で円（半円）を描いて定義していましたね。

三角方程式の問題でも、単位円を用いて攻略していきます。

解答

(1)

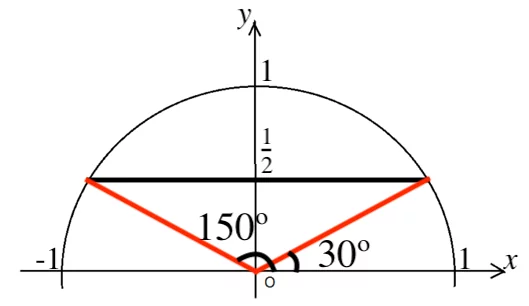
図より θ = 30º, 150º

(2)

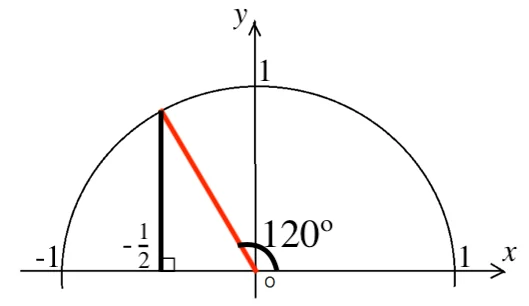
図より θ = 120º

三角比を用いた方程式の問題２

問題

のとき、θ の方程式  を解け。

方針

複雑な方程式になりました。

正弦 (sin) と余弦 (cos) の双方があると処理しきれないので、まずは片方のみの式に直しましょう。

 の関係式が活躍します。

解答

より    

左辺を因数分解して

したがって または

のとき θ = 60º であり、 のとき θ = 180º

よって方程式の解は θ = 60º, 180º

式の値を求める問題

問題

 のとき、次の式の値を求めよ。ただし、とする。

(1)

(2)

(3)

方針

超頻出。学年末試験で三角比が試験範囲になっている人は、この問題を絶対に復習しましょう。

解答

(1)

与えられた式の両辺を 2 乗すると、

となる。 を用いると、上式の左辺は  となるので、

(2)

3 乗 - 3 乗の因数分解の公式を用いると

となる。ここで与えられた式や (1) の結果、それに  を用いると

(3)

であるため、(1) の結果も用いると

となる。ここで より sinθ ≥ 0 であり、sinθcosθ > 0 となっているので cosθ > 0 である。

よって sinθ + cosθ > 0 なので、

三角不等式１

問題

のとき、次の不等式を満たす θ の値の範囲を求めよ。

(1)

(2)

(3)

方針

先ほどは方程式を扱いましたが、今度は不等式です。

境界値だけでなく「どちら側か」にも注目します。

正接 (tan) の場合は、定義域にも注意しましょう。

解答

(1)

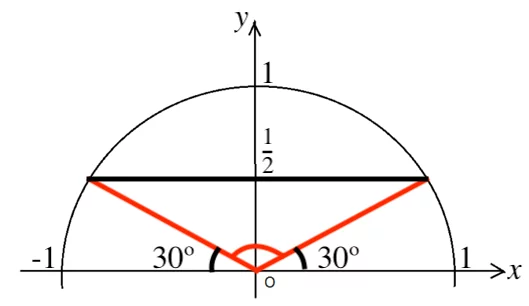
上図において、半円弧のうち直線 よりも上側にある部分に対応する θ の範囲を求めればよい。

よって

(2)

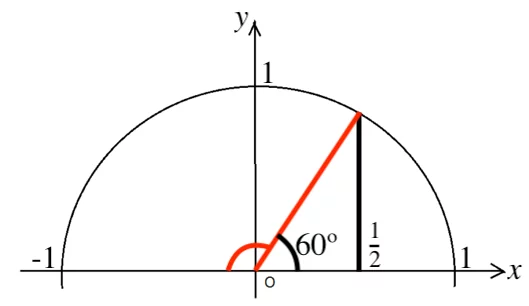
上図において、半円弧のうち直線 よりも左側にある部分に対応する θ の範囲を求めればよい。

よって

(3)

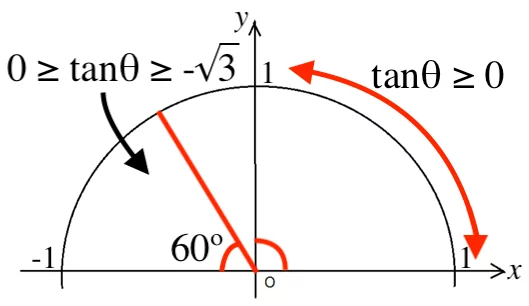
まず 0º ≤ θ < 90º では tanθ ≥ 0 なので不等式が成立する。

また 120º ≤ θ ≤ 180º のときは 0 ≥ tanθ ≥ -√3 となり、こちらも不等式が成立する。

tanθ ≥ -√3 となる θ の範囲は上図の通りであるため、

三角不等式２

問題

のとき、不等式  を解け。

方針

今度は三角比単体ではなく、複雑な形の不等式です。

方程式の場合同様、１種類の三角比のみで表現します。

解答

 であるため、

ただし  であるため、

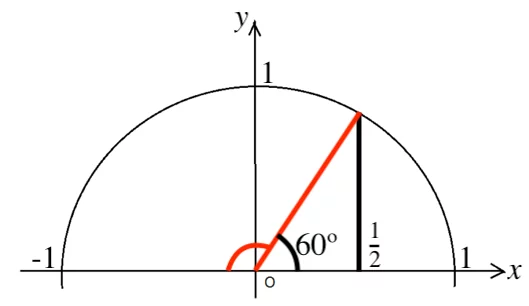
となるような θ の範囲を求めればよいので、上図より 60º < θ ≤ 180º

三角比を用いた二次関数の最大値・最小値

問題

 のとき、 の最大値・最小値、およびそのときの θ の値を求めよ。

方針

三角比の応用問題として最も定番なものですね。

まずは正弦 (sin) または余弦 (cos) のみの式で表し、それを二次関数とみて最大点・最小点を調べていきます。

解答

であるため、

これは と変形でき、sinθ = t とおくと  と書ける。

ただし なので であることに注意する。

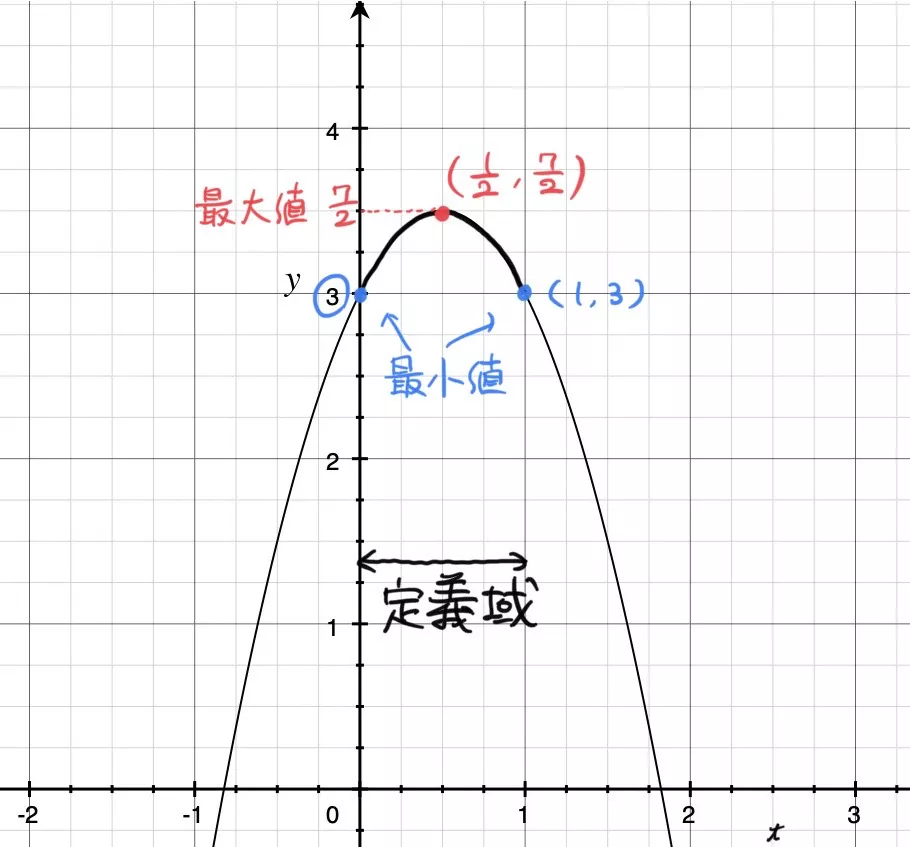
 のグラフは上図のようになる。よって、

つまり θ = 30º, 150º のとき最大値

t = 0, 1 つまり θ = 0º, 90º, 180º のとき最小値 3

まとめ

三角比の方程式や不等式、二次関数の定番問題を扱いました。

重要なものばかりなので、全ての問題を解けるようにしておきましょう。

今回扱わなかった面積関連の問題は、次の記事で扱っています。

こちらもあわせてご覧ください：