スタクラ情報局
2021.03.01
三角比を用いた計算問題をマスターしよう！
三角比を用いた計算
この記事では、三角比を用いた種々の計算問題を扱います。
定義のおさらい
まずは、三角比の定義を復習しておきましょう。
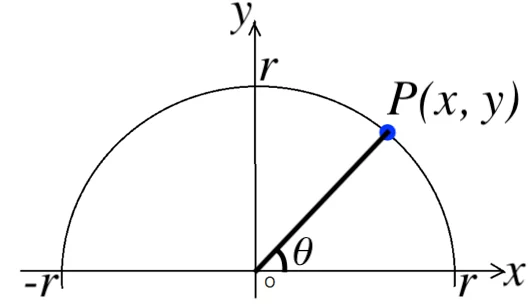
座標平面上で、原典を中心とする半径 r の円弧を考えます。
円弧上で、x 軸正方向からの角度 θ のところにある点を P (x, y) としたときに、
と定義するのでした。また、
と定義します。
※数学 I の範囲では 
となっていますが、学校によっては 
で教えているところもあります。
暗記必須の三角比の値
必ず覚えておくべき三角比の値を表にまとめました。
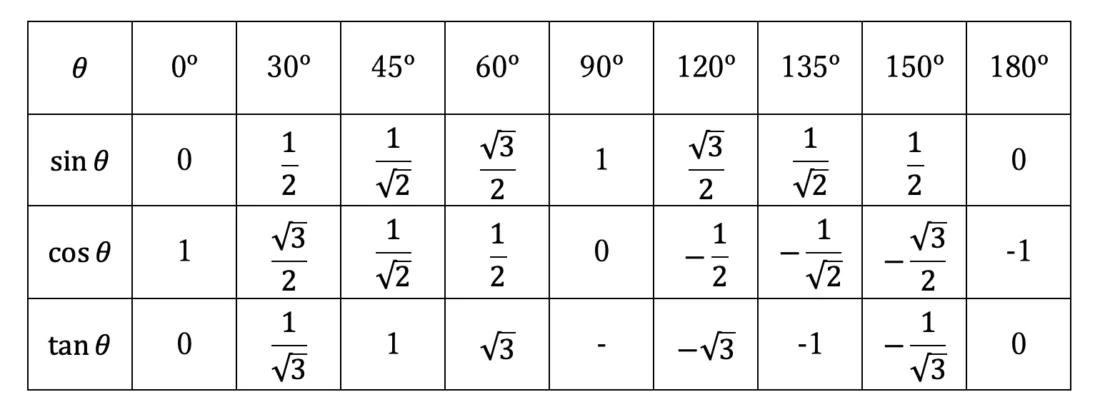※ 90º での正接（tan）の値は定義されません。
これらの値は、いつでも計算に使えるようにしておきましょう。
基本公式のおさらい
次に、三角比の基本公式を復習します。
相互関係
異なる三角比の間には、次のような関係が成り立ちます。
一つ目の式は正接（ tan ）の定義から直ちにしたがうものです。
二つ目の式は、三平方の定理を用いると証明できます。
先ほどの図で 
が成り立つことを用いましょう。
三つ目の式は、二つ目の式を 
で割り算したものです。
90º - θ や 180º - θ の三角比
90º - θ や 180º - θ の三角比の計算をおさらいします。
単位円を描いて、上の公式を確かめてみましょう。
三角比の計算問題をマスターしよう！
ではいよいよ、三角比の計算問題を見ていきます。
様々な三角比の四則演算
例題
の値を求めよ。
解答
であり
なので 
同様に 
であるため、
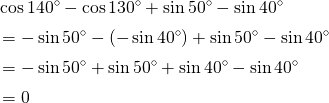
ポイント
こうした様々な三角比の足し算引き算は、ほぼ確実にシンプルな答えになります。
180º - θ の三角比などを思い出して、一つ一つ丁寧に式変形していきましょう。
途中で符号や sin, cos のミスがあると途端に複雑になってしまいます。
逆に、複雑な結果になってしまったら「どこかで計算ミスをしていないかな？」と自分でチェックするようにしましょう。
等式を証明するもの
例題
が成り立つことを証明せよ。
解答
であるから
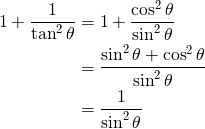
より示された。ただし、途中で 
を用いている。
ポイント
等式の証明問題は、三角比の相互関係を用いて証明していきます。
上の問題では右辺を左辺に変形していきましたが、どちらが平易かは問題次第。
複雑な方からスタートして式変形をし、簡単な方に変形してクリア、というのがよくある流れです。
sin, cos, tan の値を計算するもの
例題1
θ が鋭角で 
であるとき、
、
の値を求めよ。
解答
であるため、
であるため、
また 
例題2
θ が鋭角で 
であるとき、、
の値を求めよ。
解答
であるため、
したがって
であるから
また であるから
ポイント
三角比の相互関係を用いて他の三角比を求める場合、符号の選択をする必要があります。
角度の範囲に注意して、適切な符号を選択しましょう。
いつもプラスが正しいとは限らないので要注意です。
式の値を計算するもの
例題
とする。
のとき、次の式の値を求めよ。
(1) 
(2) 
(3) 
解答
(1)
の両辺を二乗すると
も合わせると
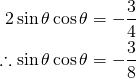
(2)
(1) の結果を用いると、
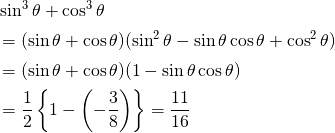
(3)
のとき 
であるから、
より 
ゆえに 
(1) より 
よって、
ポイント
(1) で の両辺を二乗するのが山場。
知らないとなかなかできない式変形ですね。
二乗して 
と 
を出して を用いることで、 だけが残るというカラクリです。
三角比の式の値を求める問題では重要ポイントなので、必ず覚えておきましょう。
(2) の三乗＋三乗は、因数分解の公式を活用します。
(3) でも (1) の考えを応用し、
を計算していきます。
まとめ
三角比を用いた代表的な計算問題
様々な三角比の四則演算
等式を証明するもの
sin, cos, tan の値を計算するもの
式の値を計算するもの
についてまとめました。
特に式の値を求める問題などでは、図を描いても意味がないことがあります。
三角比の相互関係を利用して淡々と計算すれば確実に答えにたどり着けますし、図を描いて角度 θ の位置を知っても問題解決につながらないためです。
本記事で取り上げた問題はどれも定期試験頻出。確実に解けるようにしておきましょう！