ルートの計算方法～定義から応用問題まで

中学 3 年の数学で登場する「ルート（根号）」。

これまでに扱ってきた数とは一味違う、ちょっと難しい数です。

しかしこのルートは

• 二次方程式を解くとき
• 三平方の定理で直角三角形の辺の長さを求めるとき

など重要な場面で頻繁に登場します。

そこで今回は、ルートが登場する問題の計算方法をご紹介します。

今後の数学で重要になるルートを、この記事でマスターしちゃいましょう！

平方根・ルート

まずは平方根・ルートの定義について見ていきましょう。

平方根とは

ある数 A を与えたときに、2 乗すると A になるような数のことを、A の平方根といいます。

例えば 4 の平方根とは、2 乗すると 4 になる数のことです。

であるため、2 も -2 も 4 の平方根です。

中学数学の範囲では、0 以上の数にしか平方根が存在しないことに注意しましょう。

※ 0 の平方根は 0 のみです。

ルートとは

いよいよルートの登場です。

ある数 A (A > 0) の平方根のうち負でないものを と書き、「ルート A 」と読みます。

例えば を 2 乗すると 3 になります。

また を 2 乗すると 4 になるわけですが、 だったので は 2 にほかなりません。

※ の記号単体は「根号（ルート）」とよびます。

 

ここで注意点。

「平方根」と「ルート」は別物です。

ある数 A の平方根とは、2 乗すると A になるような数全てを指しますが、 はそのうち負でないもののみを指します。

例：
・ と 2 は等しいですが、 と -2 は異なる数です。
・4 の平方根は +2 と -2 です。
・ は正しいです。

ルートの中身を簡単にする方法

ルート関連の問題では、ルートの中身を簡単にするという操作が必須です。

次はその計算方法をご紹介します。

中身が平方数の場合

先ほど という例が登場しました。

4 は平方数（同じ整数の 2 乗で表される数）の一つです。

このようにルートの中身が平方数になっているときは、ルートの計算が簡単になります。

 

0 以上の整数 n に対し、 を計算することを考えましょう。

ルートの定義を思い出すと、この数は「 2 乗したら  になる数のうち負でないもの」ですね。

ここで n という数を 2 乗すると、ちょうど  となります。

したがって であることがわかりますね！

※ n = 2 とすると という式が出てきます。

中身が平方数でない場合

次は、中身が平方数でない場合を考えましょう。

例えば  を簡単にすることを考えます。

 

まず大切なのは、ルートの中身を素因数分解することです。

素因数分解とは、正の整数を素数の積で表現することでした。

18 を素因数分解すると、 となります。

 

次に、複数個含まれている素因数に着目します。

今回の場合 "3" が二個存在しますね。

この二個の 3 をルートの外に出し、 とすることができるのです。

これがまさに「ルートの中身を簡単にする」という操作ですね。

実はこれ、先ほどの  と同じことをしています。

2 が余計に加わっていますが、n = 3 とした場合に相当しています。

 

上の計算で正しいのか確認してみましょう。

計算結果として出てきた を 2 乗してみると

となり、確かに 18 になっています。

とは「 2 乗すると 18 になる負でない数」のことでしたから、 であることが確認できました。

 

ルートの中身を簡単にする方法をまとめると次のようになります：

1. ルートの中身を素因数分解する
2. 複数ある素因数のうち二個をルートの中から取り去り、一つをルートの外につける。

この手順は今後数学で山ほど用いるので、今ここで頭に入れてしまいましょう。

 

その他の例：

二つ目の例のように、素因数が 2 個あれば何回でも取り出すことができます。

2 だけ取り出すと となり、3 だけ取り出すと となりますが、これらは全て等しい数です。

解答するときはできる限り簡単にしなければいけないので、 が正解となります。

ルートの中身を簡単にするときの注意点

 を簡単にすることを考えます。

8 を素因数分解すると  となります。

先ほどの手順にしたがってルートの中身を簡単にすると  となります。

ルートの中には素因数 2 が三個ありますが、中身を簡単にするときは二個ずつしか取り出せないことに注意しましょう。

すべて取り出して  とするのは誤りです。

 

を簡単にすることを考えます。

35 は素因数分解すると となりますが、素因数 5 も 7 も一個ずつしか含まれていません。

こういう場合は、これ以上簡単にすることができません。

有理化

これまでは、シンプルなルートの中身を簡単にする方法を紹介してきました。

次はルートが登場する分数の分母を有理化する計算方法について説明します。

「分母を有理化する」とは、「分母にルートが含まれないようにする」ことと心得れば OK です！

 

例えば を簡単にすることを考えましょう。

いまのところ分母には があるので、これを取り払います。

分母からルートをなくすには、ルートの性質を利用すれば OK。

 分母・分子の両方に をかけてみると、次のようになります。

分母は  ですが、 は「 2 乗すると 2 になる負でない数」ですので、 となります。

したがって分母からルートがなくなり、上の計算が成り立つわけです。

 

同様に、例えば次の計算が成り立ちます：

足し算・引き算

さらに、足し算・引き算も織り交ぜたルートの計算方法を見ていきましょう。

 

問題

次の式を計算せよ。

---

解答

であるため、

となる。

---

ポイント

一気に全て処理しようとせず、まずは各項を簡単にしましょう。

まずノートに を簡単にする計算をし、最後にそれを用いて計算するという流れです。

特に不慣れなうちは、1 つ 1 つ慎重に計算していくのが大切です！

四則演算を織り交ぜたもの

ちょっとレベルの高い問題として、少し複雑な計算問題も見ておきます。

 

問題１

 を計算せよ。

---

解答

---

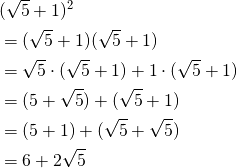
ポイント

ルートもそうでない数も含まれていますが、全ての組み合わせで掛け算してそれを足し合わせれば OK です。

次図を見ると理解しやすいかもしれません。

どうしを掛け算すると、ルートの定義より  となることを思い出しましょう。

答えにもルートとそうでない数が混在します。

 

問題２

 を計算せよ。

---

解答

---

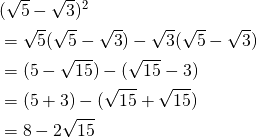
ポイント

先ほどの問題同様、掛け算を丁寧にばらしていきます。

 となるのがポイント。

より一般に、二つの数 について  が成り立ちます。