二次関数のグラフの書き方とグラフの問題

数学 I の花形分野である「二次関数」。

その中でも、今回は「グラフ」がテーマです。

二次関数のグラフはどういうものなのか。どうやって描けばいのか。グラフ関連の問題はどう解けばいいのか。

その辺りを詳しく説明していきます。

二次関数のグラフとはどういうものか

一次関数のグラフは、座標平面で直線でしたね。

二次関数のグラフの形状は「放物線」といい、次のような見た目です：

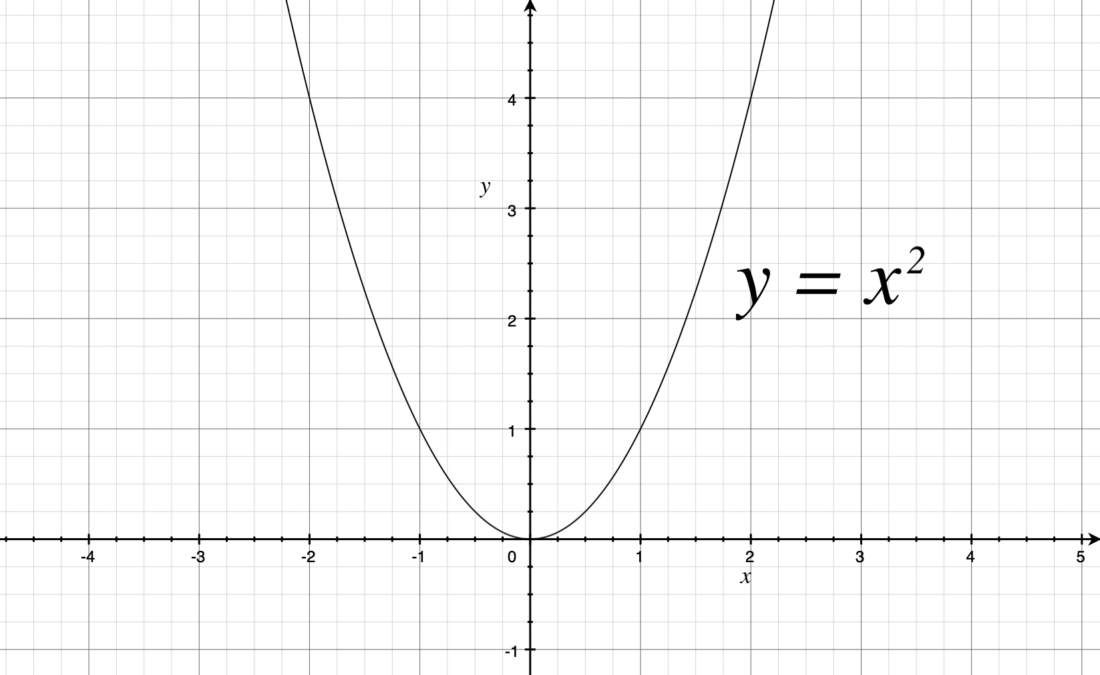
※最もシンプルな二次関数である のグラフです。

 

物を投げたときの軌道がこういう形をしているので、放物線と呼ばれています（今回は上下逆ですが…）

放物線は、円弧などとは異なる特殊な形をしているので注意しましょう。

放物線の対称の中心（今の場合は y 軸）のことを放物線の軸といいます。

また、放物線のてっぺんや底（今の場合は原点）のことを頂点といいます。

二次関数のグラフの基礎知識

ではここから、二次関数のグラフの具体的な描き方を紹介していきます。

二次の係数のみあるタイプ

まずは、二次の係数のみあるタイプから。

中学校の数学でも登場した、 というものです。

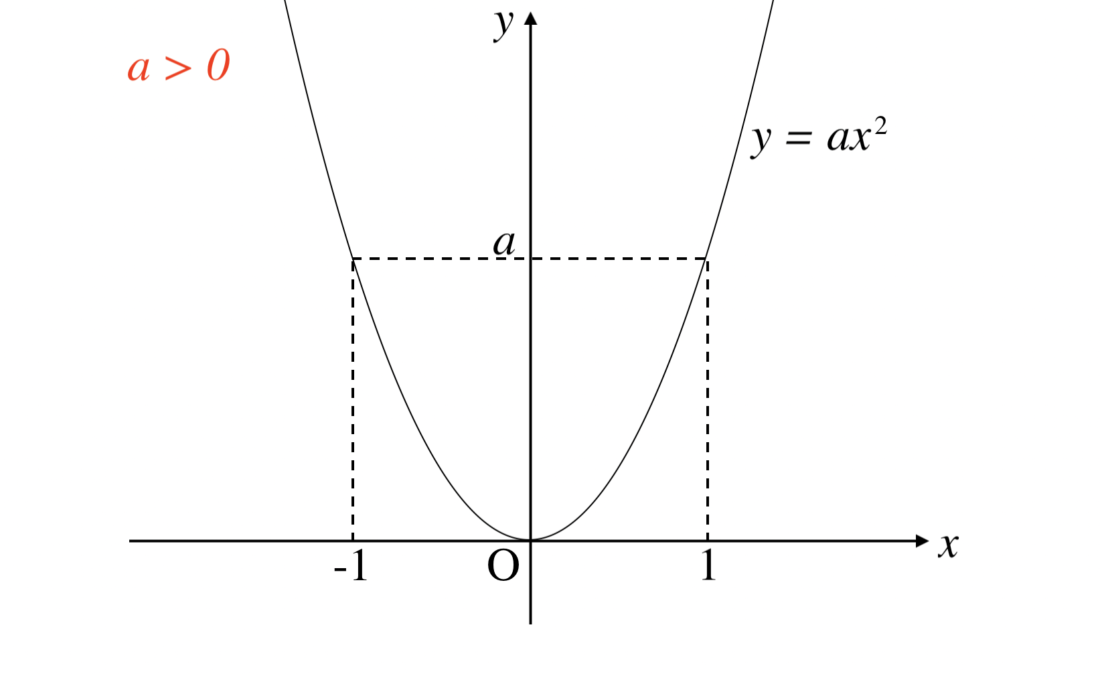
a > 0 の場合は上の通りで、「下に凸」（したにとつ）の放物線となります。

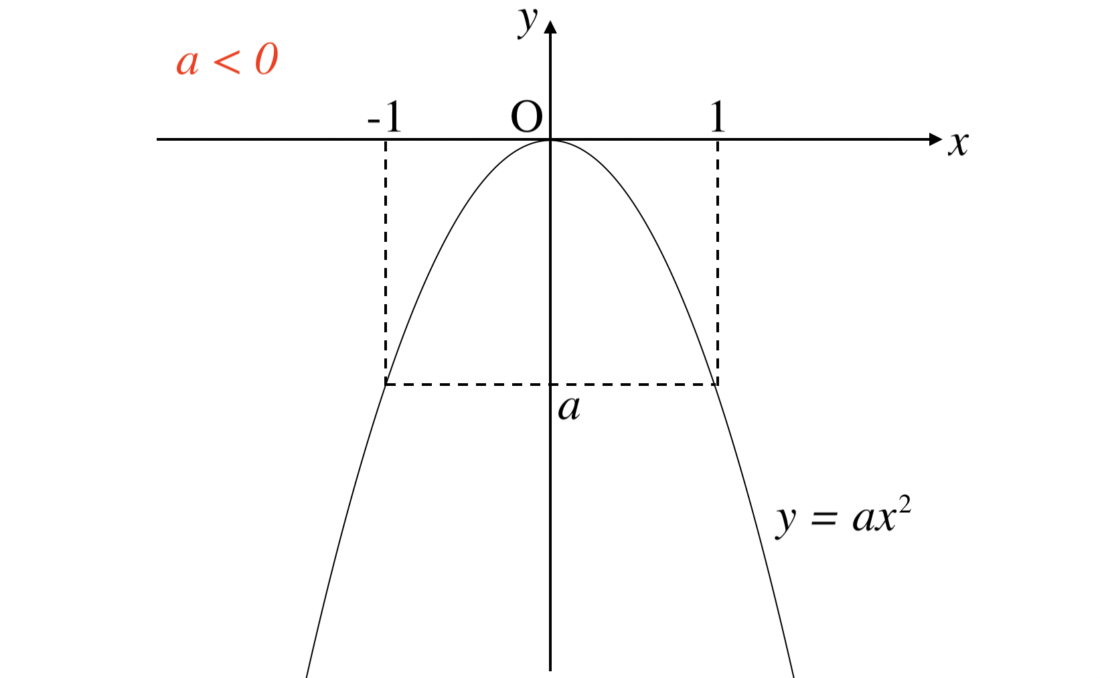
a < 0 の場合は上の通りです。

こちらは「上に凸」（うえにとつ）と表現します。

 

いずれの場合も軸は直線 x = 0 （つまり y 軸）であり、頂点は点 (0, 0) です。

 

二次の係数のみある場合、二次関数のグラフは y 軸に関して対称になります。

a の符号によってグラフの向きが変わるので注意しましょう。

二次関数の一般形とその変形（平方完成）

次に、二次関数の一般形について説明します。（ここからが本番）

先ほどはシンプルな形を紹介しましたが、実際はもっとたくさんの種類があります。

最も一般的な形で書くと です。

二次の係数も一次の係数も、定数もあるパターンですね。

という二次関数のグラフを描くには、どうすれば良いでしょうか。

 

ポイントは「平方完成」にあります。

はすでに平方完成が済んでいる形だったからこそ、原点が頂点になるとすぐわかるのです。

したがって、二次関数  も平方完成してみましょう：

というふうに平方完成できるので、二次関数  は

となりました。

平方完成した形から、グラフの頂点・軸がわかる！

平方完成する意味を述べていませんでしたね。

 → 

この形まで変形してきました。

ここで、平方完成した後に残った に着目すると、ここには x が含まれていません。

x によらない定数ということになります。

x によって変化するのは、結局 の部分だけですね。

例えば a > 0 の場合を考えましょう。

実数の二乗は必ず 0 以上なので、 が成り立ちます。

また、この等号は のときに成立します。

 

したがって、関数 は で最小値 をとるということがいえるのです。

a > 0 のグラフで最小値をとる点は、頂点に他なりません。

以上より、二次関数 の頂点は点  とわかりました。

軸は直線 です。

※a < 0 でも頂点の座標は同じになります。

グラフの平行移動

グラフ関連の問題で重要なのが、グラフの平行移動です。

 

---

関数 のグラフ F を x 軸方向に p 、y 軸方向に q だけ平行移動して得られるグラフ G の方程式は  となる。

---

 

大まかな証明：

のグラフ上の点を x 軸方向に p 、y 軸方向に q 平行並行移動したら、点 (X, Y) になったとする。

移動前の点の座標は (X - p, Y - q) となる。

移動前のグラフの方程式は であったから、移動後のグラフの点 (X, Y) が満たすべき方程式は である。

以上より、移動後のグラフの方程式は  となる。

 

これを用いると、例えば二次関数 のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動して得られるグラフの方程式は

とわかります。

ここまでのまとめ

二次関数のグラフは放物線という形をしている。

二次の係数 a が正のときは下に凸、負のときは下に凸となる。

二次関数 のグラフの軸は直線 であり、頂点は点  である。

 

二次関数 のグラフを x 軸方向に p 、y 軸方向に q だけ平行移動して得られるグラフの方程式は  である。

二次関数のグラフ関連の問題

という訳で、ここまで二次関数のグラフの基礎を説明してきました。

内容としては事足りているのですが、文字ばかりでイメージしにくかった人もいるかもしれません。

そこで、以下は具体的な問題演習をしていきましょう。

グラフを描く問題

まずはシンプルに、グラフを描く問題から。

先ほどの説明と同じように、平方完成して頂点の座標を求めます。

 

---

問題
二次関数 のグラフを描け。

---

解答

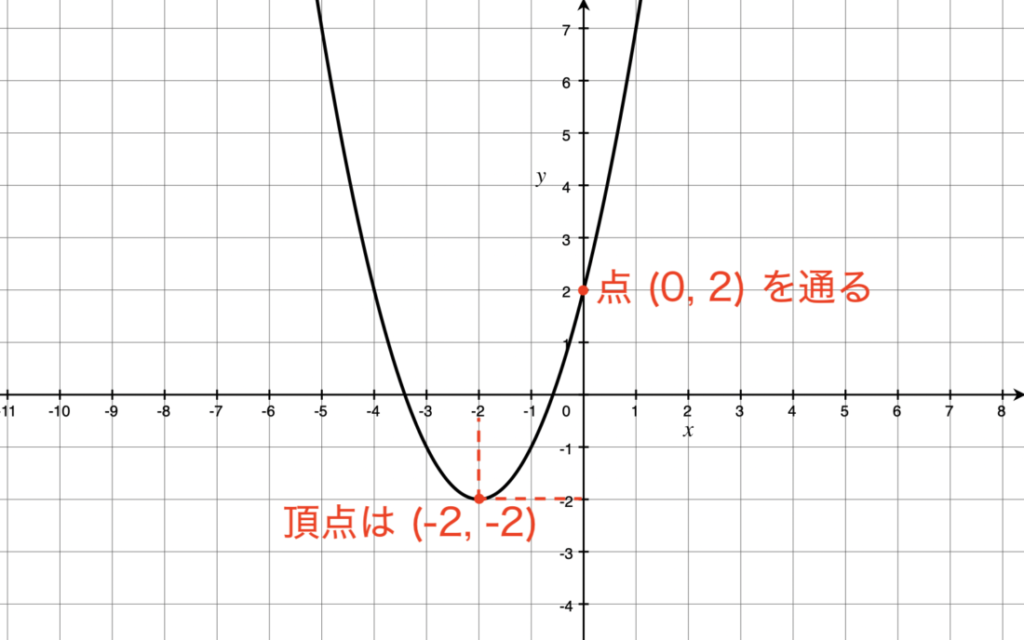
であるため、グラフの頂点の座標は (-2, -2) となる。

よって、グラフは次の通り。

 

ポイント・注意点

頂点の座標を示すだけでは、二次関数は決定できません。

頂点およびそれ以外にグラフが通る 1 点の座標が判明して、初めて二次関数を決定できるのです。

したがって、グラフを描く問題でも頂点以外に 1 点を示すようにしましょう。

x = 0 の点や y = 0 の点を書き込んでおくのが無難です。

放物線は手書きしにくい形をしているので、方眼紙に練習しておくと良いでしょう。

 

 

二次の係数が負である場合も同様です。

---

問題
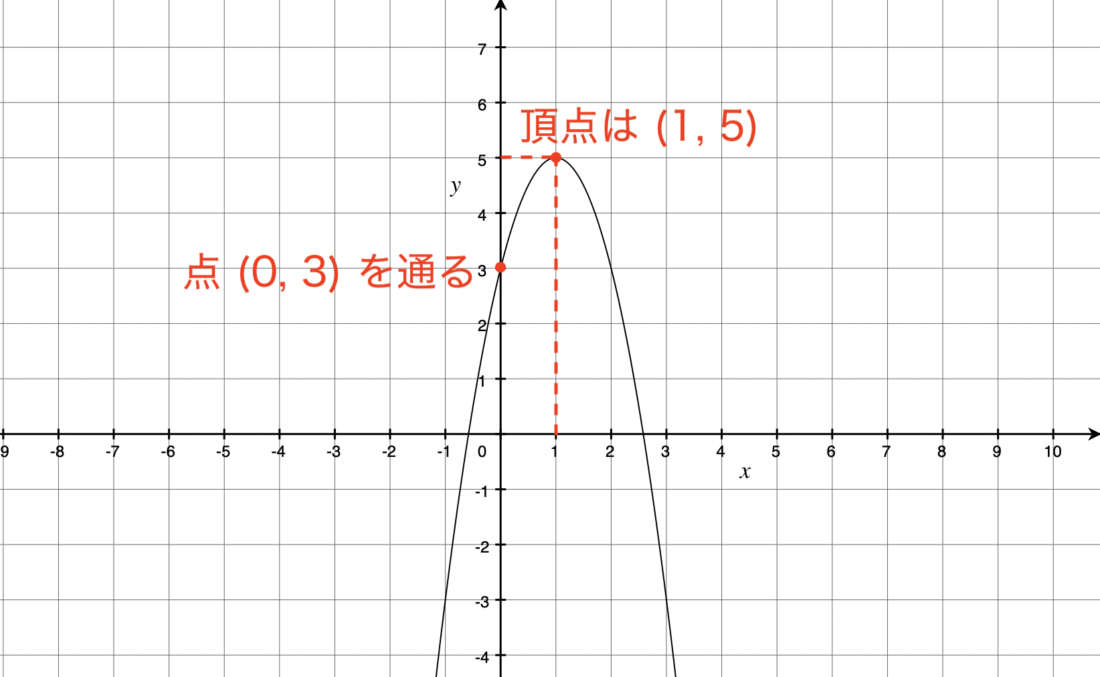
二次関数  のグラフを描け。

---

解答

この二次関数は と平方完成できる。

したがって、グラフの頂点の座標は (1, 5) となる。

グラフの位置から係数等の符号を計算するもの

今度はグラフが与えられていて、そこからいろいろ読み取る問題です。

よくある問題ですが、初見だと頭を使う必要があります。

---

問題
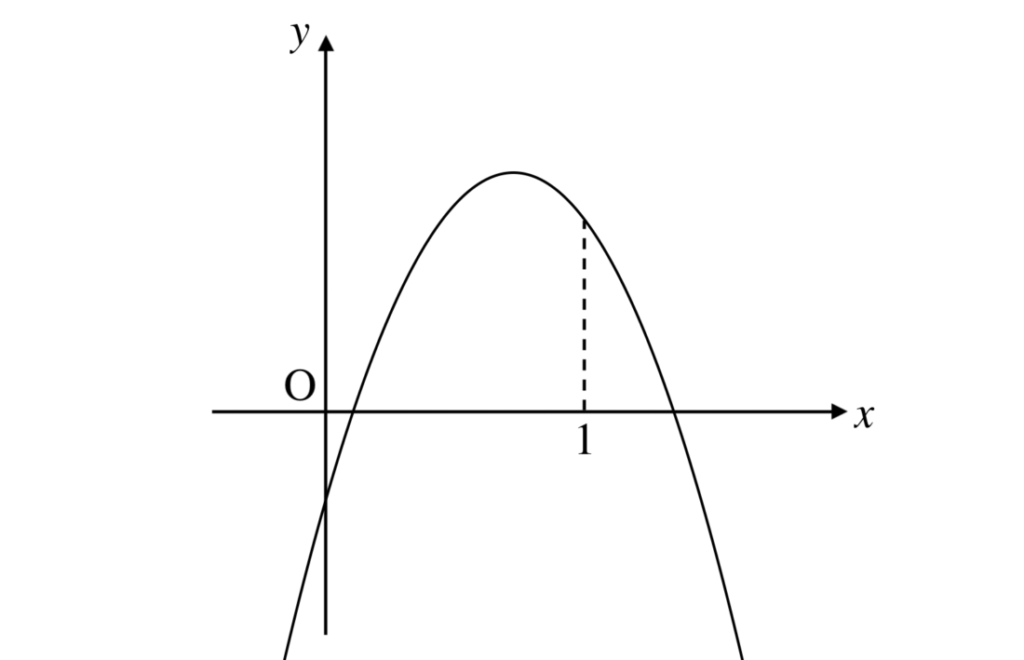
二次関数  のグラフが右の図のようになるとき、次の値の符号を調べよ。

(1) a
(2) b
(3) c
(4) a + b + c
(5) a - b + c
(6)

---

解答

 としておきます。

(1) グラフは上に凸となっているので、a < 0 である。

(2) グラフの頂点の x 座標は であり、上のグラフの頂点は x > 0 を満たす。いま a < 0 なので、b > 0 となる。

(3) このグラフは y 軸の y < 0 の部分と交わっている。よって  である。

(4) グラフより  である。 であるため a + b + c > 0 となる。

(5) グラフより  である。 であるため a - b + c < 0 とわかる。

(6) グラフより、頂点は y > 0 を満たしている。この二次関数の頂点の座標は と書けることおよび a < 0 も合わせると、 とわかる。

 

ポイント

一見情報量が少ないグラフですが、軸との交点などをよく見ることで様々な式の符号がわかるのです。

どこに着目するかは慣れないと難しいので、ぜひこうした問題を自力で解いてみてください。

グラフの平行移動

二次関数のグラフの平行移動に関する問題もご紹介しておきます。

---

問題
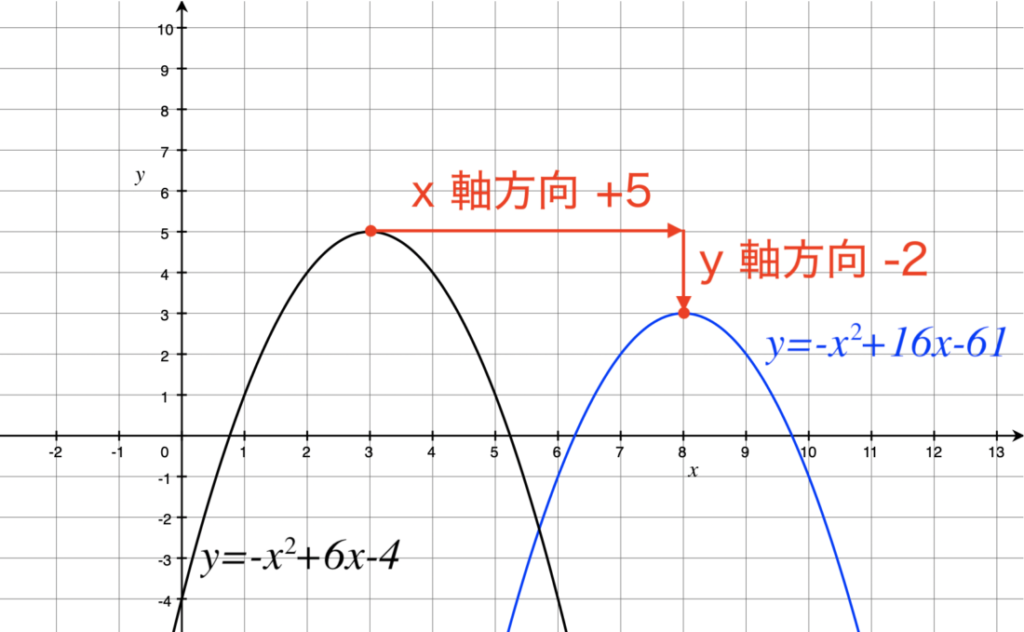
放物線 を x 軸方向に +5、y 軸方向に -2 だけ平行移動して得られる放物線の方程式を求めよ。

---

解答

平行移動して得られる放物線は  となる。これを整理し、

 

なお、各々のグラフは次のようになります。

まとめ

二次関数のグラフの描き方や、グラフに関係した問題を紹介しました。

グラフを描くためにはまず軸・頂点の情報が必要で、そのために関数の平方完成をするのでしたね。

平方完成は二次方程式の解の公式の導出にも登場した重要なテクニックなので、覚えておきましょう。

二次関数の形を見ただけで、グラフの大まかな位置を計算できるレベルまで実力を磨きましょう！

 

グラフが描けたら、二次関数の最大値・最小値問題にアプローチすることも可能になります。

二次関数の最大値・最小値についてはこの記事で扱っているので、こちらもぜひご覧ください。