スタクラ情報局
確率の計算ができないキミへ（数学A）
確率の計算の基礎
確率の計算ができない。
そう悩む人は多いのではないでしょうか？
数学A の「確率」の分野は、基本さえ理解すれば簡単ですが、それまでが大変。
確率がきっかけで数学が嫌いになってしまう人もいるはずです。
そこでこの記事では、数学A の山場の一つ「確率」の基本をお伝えしていきます。
以下の内容をゆっくり読めば、確率の計算ができるようになるでしょう。
「同様に確からしい」ということ
まずは、確率の重要概念である「同様に確からしい」ということについてお話しします。
飛行機に乗ったことはありますか？
沖縄や海外などに旅行するときはほぼ必ず使いますよね。
でも、飛行機で事故に遭ったことのある人はそういないはずです。
- 飛行機が落ちる
- 飛行機が落ちない
の 2 通りある訳ですが、飛行機が落ちる確率は絶対に 1/2 ではありません。（もしそうだったら、世の中大変です。）
つまり、何も考えずに事象を列挙し、それらの確率を等しいと仮定するのはダメなんです。
等しい確率になるまで分解する
とすると、確率の計算で重要になるのは
「等しい確率の要素まで分解する」
ということなんです。
例えば、サイコロを振ると以下の 6 つの事象のうちいずれか 1 つが起こります。
- 1 の目が出る
- 2 の目が出る
- 3 の目が出る
- 4 の目が出る
- 5 の目が出る
- 6 の目が出る
さらに、これらが起こる確率は（通常のサイコロであれば）等しく、各々 1/6 です。
このように、発生確率が等しいことを「同様に確からしい」といいます。
サイコロを振る時も、コインを投げる時も、この考え方がベースになっています。
「同様に確からしい」から、確率の計算ができる
「同様に確からしい」という概念は、確率の計算のときに必須です。
例えば次のような問題を考えましょう。
例題
さいころを投げたときに、出た目が 3 の倍数になる確率を求めよ。
先ほどの飛行機の話と同じで、
- 3 の倍数になる
- 3 の倍数にならない
という 2 つのケースがあるから 1/2 、という考え方はNGです。
解答
さいころを振ったときに起こる事象は以下の 6 通りで、これらは同様に確からしい。
- 1 の目が出る
- 2 の目が出る
- 3 の目が出る
- 4 の目が出る
- 5 の目が出る
- 6 の目が出る
出た目が3 の倍数となるのは「3」「6」の 2 通りであるため、求める確率は
同様に確からしい事象までバラしたことで、確率が
（条件を満たす場合の数）／（同様に確からしい事象の場合の数）
と計算できるわけです。
だから、「同様に確からしい」事象までバラすのが重要なんですね。
漏れ・重複がないということ
同様に確からしい事象まで分解したら、あとは場合の数のカウントをします。
ただ、そこでも注意点があります。
漏れがあってはいけない
例えば次のような問題があったとしましょう。
例題
さいころを 1 個投げるとき、出目が 6 の約数になる確率を求めよ。
このとき、6 の約数に 6 自体が含まれることを忘れてしまって、次のように答えてしまったとします。
誤解答
出目は 1, 2, 3 のいずれかであれば良いので、求める確率は 
となる。
これはもちろん不正解となります。
考えられる全てのケースについて、その場合の数を足し算しなければならないためです。
場合の数の計算時に漏れがあってはいけません。
※正解は 
です。
重複があってはいけない
一方で、場合の数のカウントに重複があってもいけません。
例題
2 個のさいころを投げるとき、出目の少なくとも一方が 3 の倍数である確率を求めよ。
この問題を次のように考えたとします。
誤解答
2 つのさいころを A, B とする。
A が 3 の倍数になる確率は 1/3、B が 3 の倍数になる確率は 1/3 であるため、求める確率は 
となる。
この足し算では、A, B の双方の出目が 3 の倍数となるケースを重複してカウントしているんです。
同じ事象を複数回カウントしてしまっては、確率を正しく計算できません。
したがって、漏れがないだけではダメで、重複も回避する必要があります。
※正解は 
となります。
問題に挑戦しよう
以上の内容に注意して、実際に問題を解いてみましょう！
余事象などの知識については、問題の中で触れていきます。
コインを投げる問題１
問題
コインを 2 枚投げるとき、表が 1 枚、裏が 1 枚となる確率を求めよ。
ここでも、同様に確からしい事象にばらして考えましょう。
解答
各コインで表が出る確率と裏が出る確率は等しく、共に 1/2 である。
よって各々のコインの表裏で全て場合分けして考える。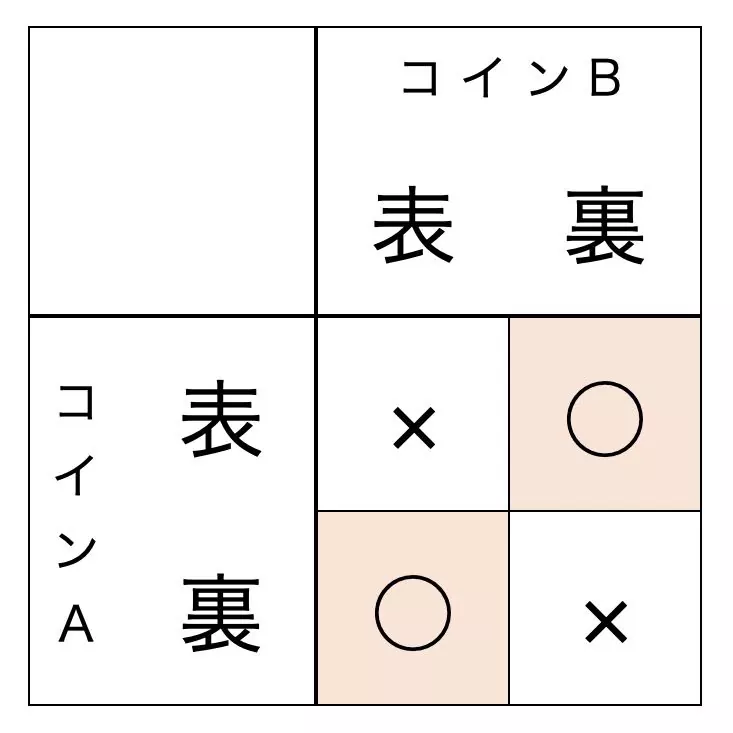
2 つのコインを A, B と名付けたときに、事象は上の表の 4 通り（= 2 x 2）あるが、これらは同様に確からしい。
表が 1 枚、裏が 1 枚出るのは上の表で色をつけた部分であるため、求める確率は 
となる。
注意
しつこいようですが、
- 2 枚とも表
- 表が 1 枚、裏が 1 枚
- 2 枚とも裏
という 3 つは同様に確からしくないので、答えは 1/3 ではありません！
コインを投げる問題２
問題
コインを 3 枚同時に投げるときに、少なくとも 1 枚は表になる確率を求めよ。
余事象も使えますが、いったん地道に考えます。
解答１
表が出ることを O、裏が出ることを X と書くことにする。
コインを順に A, B, C と命名し、各々の出目を
A が表、B が裏、C が裏 → (O, X, X)
のように表す。
3 つのコインの出目は以下の 8 通り（2 x 2 x 2）であり、これらは同様に確からしい。
(O, O, O), (O, O, X), (O, X, O), (O, X, X)
(X, O, O), (X, O, X), (X, X, O), (X, X, X)
このうち条件を満たすのは (X, X, X) 以外の 7 通りなので、求める確率は 
となる。
解答２
余事象の考え方を用いる。
「少なくとも 1 枚表が出る」の否定は「全て裏が出る」である。（これが「余事象」！）
全て裏となる確率は、
である。
したがって、求める確率は 
である。
解答２（余事象を用いたもの）も便利です。
余事象の考え方を忘れてしまった人は、教科書をよく復習してみてください。
さいころを投げる問題１
問題
さいころを 2 つ投げるとき、出目の和が 6 になる確率を求めよ。
解答
さいころを 2 つ投げるとき、全ての目の出方は 6 x 6 = 36 通りである。
そのうち、出目の和が 6 になるのは
(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)
の 5 通りであるため、求める確率は 
となる。
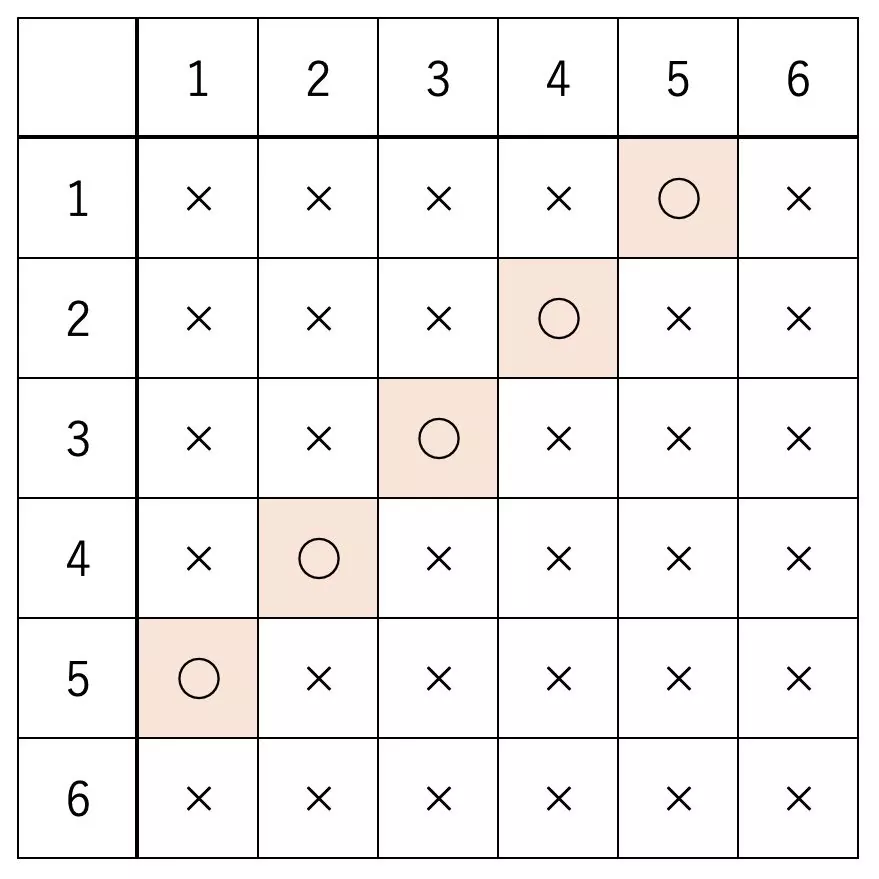
条件を満たす目の出方は、上表の色をつけた部分のようになります。
2 つのさいころを区別して 6 x 6 = 36 通りとしないと同様に確からしい事象まで分解できません。
そこに注意しましょう。
さいころを投げる問題２
問題
さいころを 3 つ投げるとき、出目の和が 6 になる確率を求めよ。
さいころの個数が増えて一見大変ですが、冷静に処理していきます。
解答
3 つのさいころの全ての目の出方は 6 x 6 x 6 = 216 通りであり、これらは同様に確からしい。
和が 6 になるような出目の組み合わせは
(1, 1, 4)
(1, 2, 3)
(2, 2, 2)
であり、並び替えを考慮すると順に 3, 6, 1 通りである。
また、これらの出目は同時に起こることがない。
したがって、求める確率は 
となる。
そのほかの確率問題
コインやさいころ以外にも、カードや文字の並び替えなど、確率問題の題材は様々あります。
問題
1 から 10 までの自然数が 1 つずつ書かれた 10 枚のカードが袋の中に入っている。この中から 2 枚を同時に取り出すとき、取り出したカードが 2 枚とも素数である確率を求めよ。
解答
全てのカードの取り出し方は 
通りであり、これらは同様に確からしい。
10 枚のカードの中で、素数は 2, 3, 5, 7 の 4 枚ある。
したがって、取り出したカードが 2 枚とも素数であるような場合の数は 
通り。
以上より、求める確率は 
となる。
まとめ
数学A の山場の一つ「確率」の計算の基礎を説明し、具体的な問題も扱いました。
確率の計算でまず大事なのが、「同様に確からしい事象まで分解すること」です。
そして、場合の数をカウントするときは
- 漏れがないようにすること
- 重複がないようにすること
の双方が大事でしたね。
以上のことを意識して数学Aの教科書等を読み直してみると、だいぶ理解しやすくなると思います。
この記事で学んだことを他の問題で実践してみてください！
