スタクラ情報局
2021.12.05
数学の苦手を克服する方法,教えます!
高校数学の苦手を克服する方法!
新型コロナウィルスの影響で,これまで一人で勉強している生徒さんも多かったでしょう。
学校で授業を受けたり質問をしたりできない分,勉強でつまずいてしまった人もいるかもしれません。
特に数学は,苦手とする生徒が多い科目です。
そこで今回は,数学の苦手を克服する方法についてレクチャーしていきます!
数学でわからない問題が増えてきた人,なんとなく数学が嫌に・面倒になってきた人はぜひ読んでください。
問題例:放物線と直線
問題
今回は,次の問題を例に説明していきます:
問題
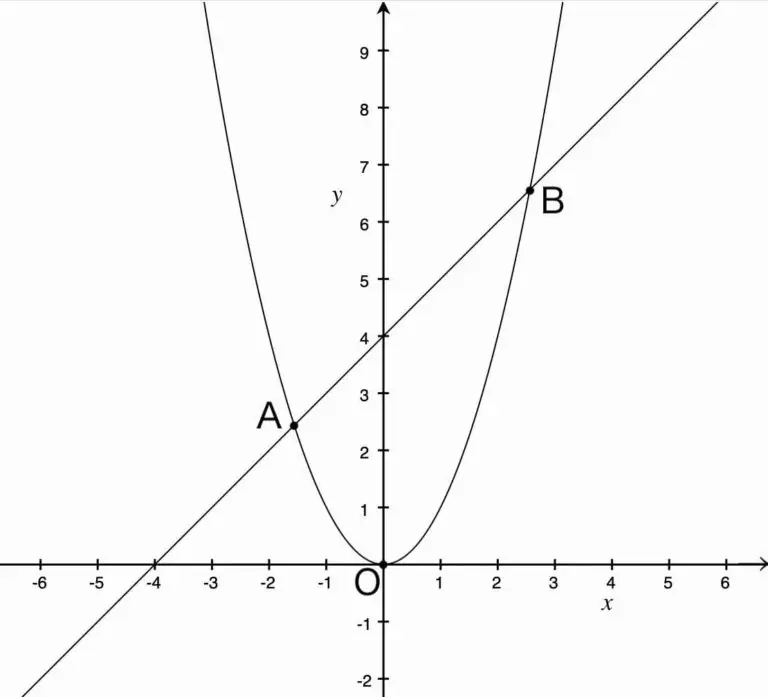
O を原点とする座標平面上に放物線 ![]() と直線
と直線 ![]() があり,これらの交点を図のように A, B とする。
があり,これらの交点を図のように A, B とする。
このとき,△OAB の面積を求めよ。
ただし,座標の 1 目盛りを 1 cm とする。
高校入試でよくある,放物線と直線に関する問題です。
これを例に,問題を解くプロセスについて詳しく分析していきます。
模範解答例
まず点 A, B の座標を求める。![]() と
と ![]() を連立することで二次方程式
を連立することで二次方程式 ![]() となり,これを解くことで
となり,これを解くことで ![]() を得る。この小さい方が A の x 座標で,大きい方が B の x 座標である。
を得る。この小さい方が A の x 座標で,大きい方が B の x 座標である。
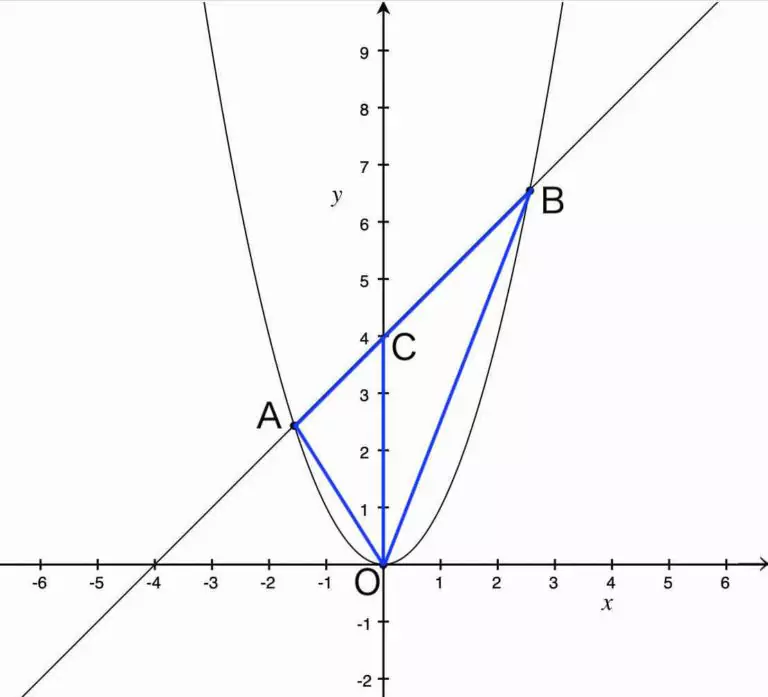
図のように直線 AB: ![]() と y 軸の交点を C とすると,C の座標は (4, 0) である。
と y 軸の交点を C とすると,C の座標は (4, 0) である。
このとき △OAB の面積は △OAC の面積と△OBC の面積の合計である。
△OAC の底辺を OC とみると,高さは点 A の x 座標の絶対値であり,その値は 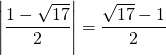 である。
である。
したがって,△OAC の面積は ![]() となる。
となる。
△OBC の底辺を OC とみると,高さは点 B の x 座標であり,その値は ![]() である。
である。
したがって,△OBC の面積は ![]() となる。
となる。
以上より,△OAB = △OAC + △OBC = ![]()
答:![]()
問題を解くステップ
以上がこの問題の解説です。
でも,今回の解説のメインテーマは問題自体ではありません。
「数学の苦手を克服する方法」が今回のテーマでしたね。
先ほどの問題を解くにあたり,どのような手順を踏んでいたのか,振り返ってみましょう。
△OAB の面積を計算するのに必要な情報を考える
今回の問題では,△OAB の面積を計算するのが目的です。
そこで,何がわかれば △OAB の面積が計算できるのか最初に予想します。
△OAB の面積を計算するにあたり,もっとも単純には 3 点の座標を特定すれば OK です。
△OAB の頂点の 1 つである原点 O は,その定義から座標が (0, 0) となっています。
なので,あとは点 A, B の座標を求めれば OK とわかります。
というわけで,次は座標計算です。
点 A, B の x 座標を特定する
△OAB の面積を計算するために点 A, B の座標を求める必要があります。
そこで,放物線の方程式 ![]() と直線の方程式
と直線の方程式 ![]() を連立します。
を連立します。
y を消去することで x の二次方程式が得られますが,この 2 つの解が A, B の x 座標となります。
連立した結果の二次方程式は ![]() つまり
つまり ![]() なので,これを二次方程式の解の公式に代入します。
なので,これを二次方程式の解の公式に代入します。
すると ![]() となりますね。
となりますね。
この座標の小さい方が点 A の x 座標,大きい方が点 B の x 座標です。
△OAB の面積を計算する
点 A, B の x 座標がわかったら,いよいよ △OAB の面積の計算をしていきます。
ただし,面積の計算はそこまで単純ではありません。
例えば 3 辺のうち 1 つが x 軸や y 軸に平行ならば,面積は容易に計算できます。
しかし今回の △OAB はどの辺も x 軸,y 軸に平行ではありません。
さらに,A, B の y 座標もまだ計算していません。
何かしら工夫をする必要があります。
そこで,先ほどの図のような点 C をとり,△OAB を 2 つの三角形に分割したのです。

このように分割すると,三角形の面積を計算しやすくなるのです。
辺 OC が y 軸と平行なので,これを底辺とみます。
すると底辺の長さはすぐ 4 とわかりますね。
直線の方程式が ![]() だからです。
だからです。
あとは,三角形の面積の公式「(底辺) × (高さ) ÷ 2」を用いるだけです。
△OAC の面積は (OC の長さ) × (A の x 座標の絶対値) ÷ 2
△OBC の面積は (OC の長さ) × (B の x 座標の絶対値) ÷ 2
で計算します。
この方法であれば,点 A, B の y 座標を計算する必要がありません。
![]() という計算で,面積は
という計算で,面積は ![]() となりますね。
となりますね。
苦手克服の第一歩は「原因の特定」
正解までのステップはたくさん
問題を解くまでの過程を一通り言葉にすると以上のようになります。
結局,![]() という答えを出すまでに,ざっと
という答えを出すまでに,ざっと
放物線と直線の方程式を連立し,二次方程式を導く
その二次方程式を解く → A, B の座標
△OAB の面積を計算する方法を考え,準備をする
△OAB の面積を計算する
というステップが必要なのです。
短い問題文に対し,解答に至るまでのプロセスはかなり長いですよね。
逆にいうと,不正解だったときの復習には注意が必要なんです。
自分に欠けている力が何なのかわかりにくいから。
単に不正解だったというだけだと,次のようにいろいろな原因が考えられます:
二次方程式の解の公式を忘れていた
解の公式に代入して計算する時にミスをした
△OABの面積の計算方法がわからなかった
△OAB の計算過程でミスがあった
自分が出した答えを解答欄に写すときにミスがあった
...
どれが原因かわからないと,対策のしようもありませんよね。
もし二次方程式の解の公式をちゃんと暗記できていないのであれば,似たような(放物線とか直線に関する)問題をたくさん解いても意味がありません。
解の公式を暗記して,それを使って二次方程式を解く練習をするのがベストなのに,それに気づかないのは時間がもったいないです。
類題を解いて,ずっと不正解,不正解,... の繰り返しでは,だんだん数学が苦手になってしまいます。
数学という科目自体が嫌いになってしまうことでしょう。
それで挫折するのはもったいないです。
数学の苦手意識の原因は,多くの場合ここにあります。
原因を特定し,対策しよう
数学の苦手克服で一番大切なこと。
それは原因を特定して,それに応じた対策を練ることです。
(これが今回のポイントです!)
単に「マルかバツか」で判断するのではありません。
正解までの道筋を細かなステップに分けて,どこで自分がつまずいたのかはっきりさせましょう。
そして,それに応じて対策の勉強をするのです。
先ほどの問題の場合,二次方程式を解いて点 A, B の座標を求める段階でミスをしているのだとしたら,二次方程式関係の練習をすることになります。
解の公式があやふやだったら,教科書に戻ってその勉強をする。
根号(ルート)の中身を計算するときにミスをしているのであれば,もうちょっと前に戻って根号の計算を練習する。
前の内容に戻るのは抵抗があるかもしれませんが,それが一番の近道です。
面倒なようでも,ちょっと我慢しましょう。
自分一人ではできない場合
でも,苦手の原因を分析してその対策をするというのは,実は結構高度なこと。
正直,それができれば勉強で苦労しませんよね。
一人でできない場合は,学校や塾の数学の先生に頼んでみましょう。
そうすれば,的確なアドバイスをもらえるはずです。
お願いするときに大切なのは,「これ採点してください!」という風に丸投げしないことです。
解答・解説が手元にあれば,採点(正解か不正解かの判断)だけは自分でできますよね。
でも,今やりたいことはそれではないはずです。
「採点はしたんですけど,どこでつまずいているのかわかりません。教えてください!」
「採点はしたんですけど,ここからどう復習すればいいでしょうか?」
という風に,原因の特定やその後の勉強に繋がるような聞き方をしてみましょう。
苦手ポイント診断テスト(高校生向け)
数学の問題を解くのには複数のステップが必要。
どのステップで自分が躓いたのかを分析し,対策をするのが苦手克服の方法。
ここまで,そういうお話をしてきました。
でも,すぐには数学の苦手ポイントを見つけられないと思います。
そこで以下は,問題を解くだけで苦手な箇所がわかる診断テストをご用意しました。
高校一年生の数学(IA)を題材にしていますが,高校生であれば全員利用できます。(高校二年生や三年生でも,数学 IA の内容に抜けがあってはいけないので。)
まず問題を解き,その後を読み進めてください。
最後まで読む頃には,数学の苦手ポイントがはっきりするはずです!
問題編
問題1
(1) 方程式 ![]() を解け。
を解け。
(2) 不等式 ![]() を解け。
を解け。
(3) 二次関数 ![]() のグラフをかけ。
のグラフをかけ。
(4) 放物線 ![]() と直線
と直線 ![]() の共有点の個数を定数 k の値によって分類せよ。
の共有点の個数を定数 k の値によって分類せよ。
問題2
(1) 鋭角 ![]() について
について ![]() となるとき,
となるとき,![]() の値を求めよ。
の値を求めよ。
(2) ![]() であるとき,
であるとき,![]() をみたす
をみたす ![]() の値を求めよ。
の値を求めよ。
(3) △ABC において ![]() のとき,角 B と △ABC の外接円の半径を求めよ。
のとき,角 B と △ABC の外接円の半径を求めよ。
(4) △ABC において ![]() であるとき,角 C を求めよ。
であるとき,角 C を求めよ。
問題3 A, B, C, D, E, F の文字が書かれた玉が 1 個ずつ,合計 6 個ある。
(1) これらの玉を円形に並べる方法は何通りあるか。
(2) これらの玉から 4 個取り出して円形に並べる方法は何通りあるか。
(3) B, C の 2 個が隣あうように円形に並べる方法は何通りあるか。
(4) これらの玉に紐を通して輪にする方法は何通りあるか。
問題4 さいころを 2 回投げる。
(1) 出た目の和が 6 になる確率を求めよ。
(2) 出た目の和が奇数になる確率を求めよ。
(3) 出た目の積が 12 になる確率を求めよ。
(4) 出た目の積が 偶数になる確率を求めよ。
問題5
(1) 1200 の(正の)約数の総和を求めよ。
(2) ![]() が整数となる最小の自然数 n を求めよ。
が整数となる最小の自然数 n を求めよ。
(3) ![]() をみたす整数 x, y を全て求めよ。
をみたす整数 x, y を全て求めよ。
(4) ![]() をみたす整数 x, y を全て求めよ。
をみたす整数 x, y を全て求めよ。
問題6
(1) AB = 6, BC = 9, CA = 7 である △ABC の内心 I とする。直線 AI と辺 BC の交点を D とするとき AI : ID を求めよ。
(2) 次の図のように,半径 6 の円と半径 4 の円が外接している。共通外接線と各円の接点をそれぞれ A, B とするとき,線分 AB の長さを求めよ。
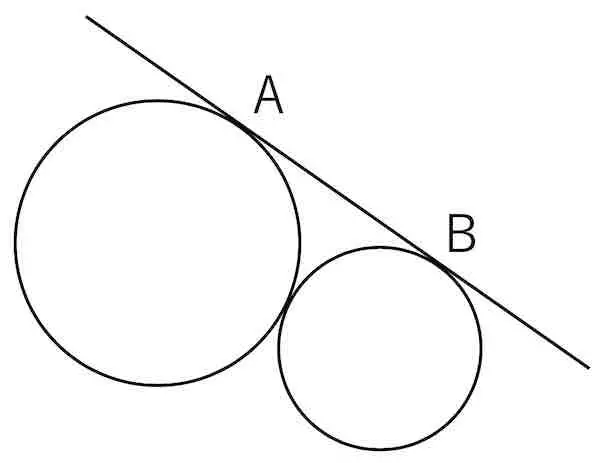
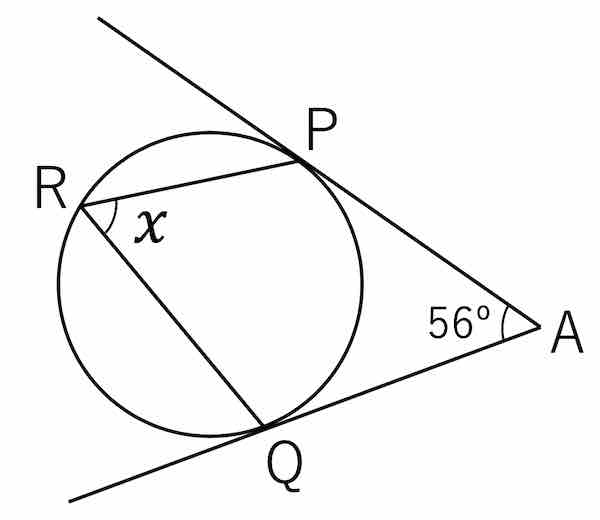
(3) 次図の角度 x を求めよ。ただし P, Q は円と直線の接点である。
(4) 一辺の長さが 6 の立方体 ABCD-EFGH において,立体 ACFH の体積 V を求めよ。
略解
まずは以下の略解で自己採点をしてみましょう。
正解か不正解かを調べれば OK です!
問題1
(1)
与えられた式の左辺を因数分解すると ![]() となるので,
となるので,![]() を解けばよい。
を解けばよい。
答: ![]()
(2)
x < -2, -2 ≦ x ≦ 0, 0 < x で分類して一次不等式を解けばよい。
答:-3 < x < -1
(3)
答: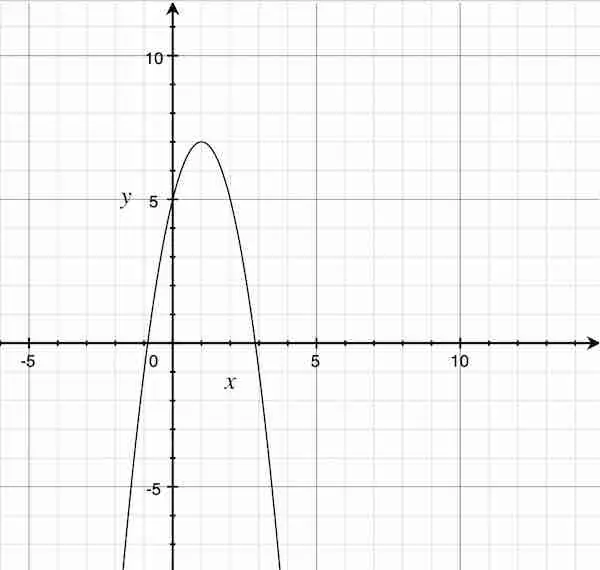
頂点は点 ( 1, 7 )
(4)
2 式を連立して得られる二次方程式 ![]() ←→
←→![]() の判別式(D とする) は
の判別式(D とする) は ![]() となる。
となる。
判別式 D の符号をもとに判断すればよい。
答え:![]() のとき 2 個,
のとき 2 個,![]() のとき 1 個,
のとき 1 個,![]() のとき 0 個
のとき 0 個
問題2
(1)
A は鋭角なので sinA, tanA の値は正であることに注意する。
答:![]() より
より 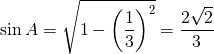 ,
, ![]()
(2)![]() において
において ![]() より
より ![]()
これを整理すると ![]() つまり
つまり ![]() となるので
となるので ![]()
![]() より
より ![]() であるため
であるため ![]() となり,これをみたす θ を求めればよい。
となり,これをみたす θ を求めればよい。
答:![]()
(3)
正弦定理より ![]() であるため
であるため ![]() であり,これより
であり,これより ![]() となる。
となる。
B は △ABC の内角であるため B = 30º, 150º であるが,A = 45º なので B = 150º は不適。B = 30º となる。
また ![]() の式の値は外接円の半径の 2 倍であるため,外接円の半径を R とすると
の式の値は外接円の半径の 2 倍であるため,外接円の半径を R とすると ![]()
答:B = 30º, (外接円の半径) = ![]()
(4)
余弦定理より ![]() である。C は三角形の内角なので
である。C は三角形の内角なので ![]() であり,
であり,![]() なので C が求まる。
なので C が求まる。
答:C = 60º
問題3
(1)
1 つの文字の玉を固定し,残りの玉の並べ方を考えればよいので,5! = 120 通り。
答:120 通り
(2)
4 個の選び方は ![]() 通り。それぞれの選び方で,玉の並べ方は (4-1)! = 6 通り。よって全部で 15 × 6 = 90 通り。
通り。それぞれの選び方で,玉の並べ方は (4-1)! = 6 通り。よって全部で 15 × 6 = 90 通り。
答:90 通り
(3)
B, C をひとまとまりと考えて "5 つ" を並べる方法は (5-1)! = 24 通り。B, C の並び替え方は 2 通り。よって 24 × 2 = 48 通り。
答:48 通り
(4)
円順列で左右反転したものは,輪を作るにあたっては同じ並び方とみなせる。よって 120 ÷ 2 = 60 通り。
答:60 通り
問題4
(1)
和が 6 になる出目は (1, 5), (2, 4), (3, 3), (4, 2), (5, 1) の 5 通りなので ![]() となる。
となる。
答:![]()
(2)
和が奇数になるのは(奇数)+(偶数), (偶数)+(奇数) のいずれかである。したがって ![]()
答:![]()
(3)
積が 12 になる出目は (2, 6), (3, 4), (4, 3), (6, 2) の 4 通りなので ![]()
答:![]()
(4)
余事象,つまり「出目の積が奇数になる」事象を考える。
このとき 2 つの出目はいずれも奇数なので,確率は ![]() である。
である。
したがって求める確率は ![]() となる。
となる。
答:![]()
問題5
(1)
1200 を素因数分解すると ![]() であるため,約数の総和は
であるため,約数の総和は ![]() となる。
となる。
答:3844
(2)
315 を素因数分解すると ![]() となる。全ての素因数の指数を偶数にすればよいので,素因数 5 と 7 を 1 つずつ増やせばよい。
となる。全ての素因数の指数を偶数にすればよいので,素因数 5 と 7 を 1 つずつ増やせばよい。
したがって求める n は ![]()
答:n = 35
(3)
例えば (x, y) = (-2, 1) は解の 1 つである。2 と 5 は互いに素であるため,一般解は ![]() ( k は整数)となる。
( k は整数)となる。
答: ![]() ( k は整数)
( k は整数)
(4)
与えられた式より ![]() となり,左辺を因数分解すると
となり,左辺を因数分解すると ![]() が得られる。
が得られる。
左辺の 2 つの因数は整数なので,![]() であり,これを解くことで (x, y) が求まる。
であり,これを解くことで (x, y) が求まる。
答:![]()
問題6
(1)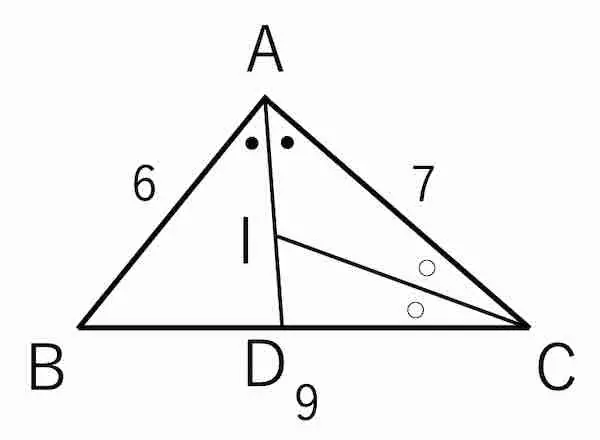
角の二等分線の性質より BD : DC = AB : AC = 6 : 7 。したがって CD = ![]()
したがって AI : ID = CA : CD = ![]() となる。
となる。
答:13 : 9
(2)
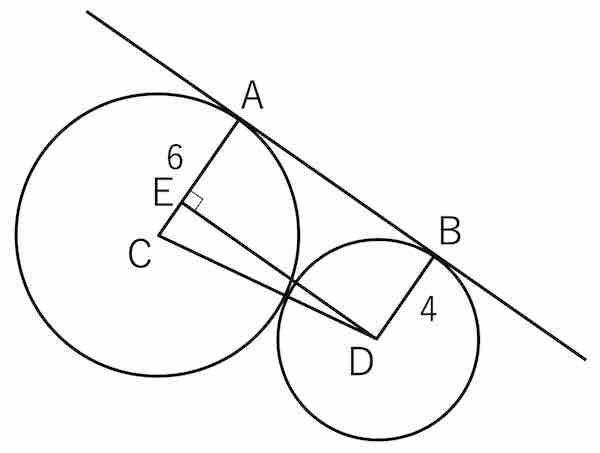
円の中心を C, D とし,点 D から線分 AC に下ろした垂線の足を E とする。
CD = 6 + 4 = 10, CE = 6 - 4 = 2 であるため,三平方の定理より DE = ![]() となる。また AB = ED である。
となる。また AB = ED である。
答:![]()
(3)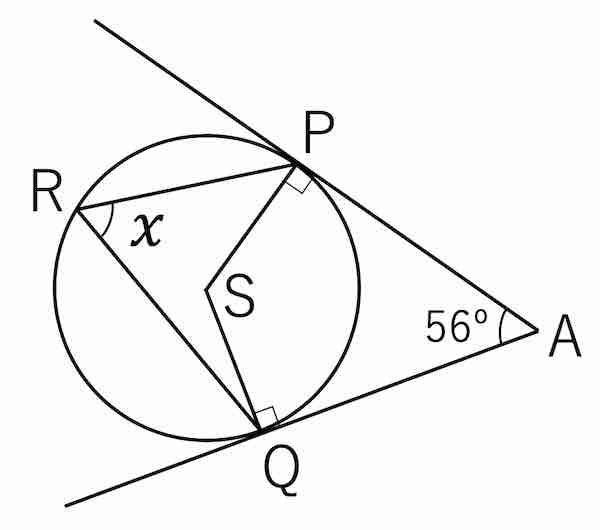
円の中心を S とする。∠APS = ∠AQS = 90º であるため,∠PSQ = 360º - (56º + 90º + 90º) = 124º である。
円周角の定理より ∠PRQ = ∠PSQ ÷ 2 = 124º ÷ 2 = 62º
答:62º
(4)
立方体の体積から,合同な 4 つの三角錐の体積を引けばよい。![]()
答:72
数学の苦手診断
いろいろな分野から 4 問ずつ出題しました。
問題と出題分野の対応は以下の通りです:
・問題1:一次関数,二次関数
・問題2:図形と計量
・問題3:場合の数
・問題4:確率
・問題5:整数
・問題6:図形の性質
どの大問も,学校の定期試験で出題されるような(そこまでハイレベルじゃない)問題を揃えてあります。
逆にいうと,これらの問題が解けていないと要復習です。
各大問で 2 問以上間違えていたら,その分野は要復習です!
すでに学習した内容であったとしても,教科書の復習から始めてみましょう。
高校二年生でも三年生でも,場合によってはここで登場した内容の復習が必要です。
前に戻るのは悔しいかもしれませんが,落ち着いて弱点を補強することで苦手が解消されます。
結果として,模試などで安定していい成績が取れるようになります。
まとめ
数学は積み上げ式の科目です。
1 つの問題を正解するまでに多くのステップが必要です。
単に正解か不正解かだけを気にしていると,理解の漏れがどこにあるのか気づけません。
だからこそ,数学の苦手克服の第一歩は「原因の特定」なんです。
問題を解くまでのステップを細かく分けて,
自分がどこまでできたのか
どこでつまずいたのか
をはっきりさせます。
そしてその次は,自分がつまずいたポイントを復習するわけですね。
これを繰り返すことで,数学の実力は確実に伸ばすことが可能です。
数学が嫌で投げ出したくなった人も,いったんここで踏ん張って,前の内容に戻ってみましょう!
