スタクラ情報局
2020.04.07
【公式いろいろ】因数分解のいろいろな問題とその解き方
因数分解～基礎から応用まで
高校の数学では，最初に「数と式」という分野を学習します（数学 I ）。
ここでは、単項式や多項式、それに整式、式の展開公式などを学びますが、その次に待ち受けているのが「因数分解」です。
因数分解は、数学 I だけでなく今後の数学でずっと登場する重要な内容です。
そこで今回は、因数分解の様々な問題を総ざらいして紹介・解説していきます。
この記事の内容をマスターすれば、高校数学もいい感じにデビューできるに違いありません！
因数分解とは
因数分解とは、1 つの整式を複数の整式の積に変形する操作をいいます。
変形後の積をなすもののそれぞれを因数と呼びます。
※整式：単項式と多項式を合わせたもの。
例えば次の例を見てみましょう。
これは最も簡単な因数分解の 1 つです。
pa + qa という整式が、p + q という整式と a という整式の掛け算に変形されています。
先ほどよりは難しい形をしていますが、これも因数分解の一例です（あとで登場します）。
基礎的な因数分解の問題を総ざらい
では次に、因数分解関連の様々な問題を紹介していきます。
全ての項に共通する因数をくくりだす
問題
次の式を因数分解せよ。
(1) 
(2) 
(3) 
解答・解説
(1) 2 つの項には因数 
が共通しているので、
(2) 2 つの項には因数 
が共通しているので、
(3) 3 つの項には因数 
が共通しているので、
ポイント
こうした最も単純なパターンの問題では、それぞれの項が文字を何個ずつ含んでいるのかを調べることになります。
例えば (1) の場合、
と 
に含まれている文字の個数は次のようになっています。
|
| |
a の個数 | 3 個 | 2 個 |
b の個数 | 2 個 | 1 個 |
そして、各文字について、含まれている個数の最小値を探します。
例えば a に着目すると、 には 3 個、 には 2 個あります。
少ないのは の方で、2 個ですね。
したがって、くくりだすことができるのは 2 個とわかります。（共通因数×何か の形にすることを「くくりだす」といいます。）
同様のことを b についても行うと、b は 1 個くくりだせることになります。
(3) のように 3 項以上ある場合も同様に、つぶさに調べていきましょう。
今回は "2" もくくりだせることに注意します。（ 1 より大きい最大公約数が存在する場合は、それもくくりだすようにしましょう。）
共通する整式を見つけだす
問題
次の式を因数分解せよ。
(1) 
(2) 
解答
(1) 
(2) 
ポイント
先ほどよりは少々難しいですが、共通する整式を見つけ出していきます。
部分部分で因数分解をしてみて、共通する整式が登場したら全体をそれでくくる、という流れです。
和の 2 乗・差の 2 乗の因数分解
公式
超重要な展開公式です。確実に頭に入れておきましょう。
どうして成り立つのかわからない場合は、右から左に展開してみることをおすすめします：
問題
次の式を因数分解せよ。
(1) 
(2) 
(3) 
(4) 
解答
(1) 
(2) 
(3) 
(4) 
たすき掛けを利用するもの
公式
2 乗の形などに簡単に因数分解できない場合は、たすき掛けを利用することになります。
正しい係数の組み合わせを探らなければならないのでちょっと大変です。
問題
次の指揮を因数分解せよ。
(1) 
(2) 
解答
(1) 下のたすき掛けより 
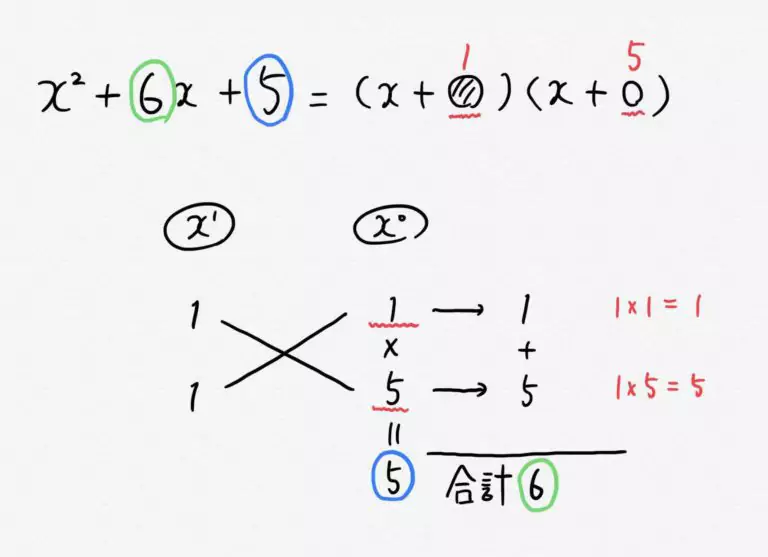
(2) 下のたすき掛けより 
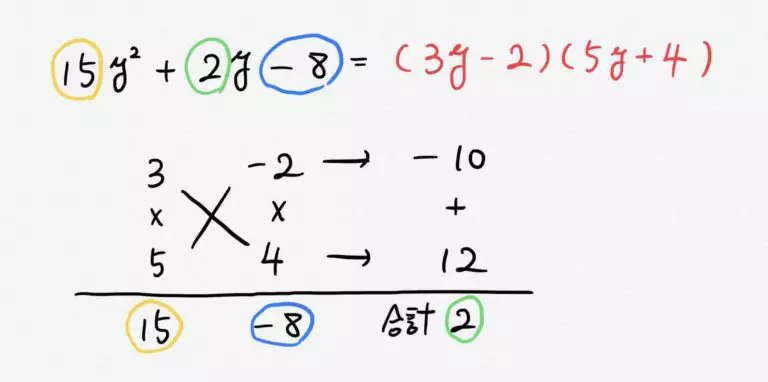
ポイント
たすき掛けを用いる計算の場合、どういう係数が適切かは手探りで求めることになります。
たくさん数をこなすことで因数分解の速度は上昇していくので、たすき掛けの計算はたくさん行うのが大切です！
和の 3 乗・差の 3 乗の因数分解
公式
2 次の場合よりも複雑になりますが、こちらも重要公式です。
符号や係数に注意しましょう！
問題
次の式を因数分解せよ。
(1) 
(2) 
解答
(1) 
(2) 
ポイント
複雑な公式ですが、公式の係数 3 に着目すると発見しやすいです。
これらの公式に限った話ではありませんが、先に展開計算の練習をしておくと楽になります。
3 乗の和・3 乗の差の因数分解
公式
どちらの公式にもプラス・マイナスの双方が登場するので、覚え間違いに注意しましょう。
ab の係数は 2 ではなく 1 です。
問題
次の式を因数分解せよ。
(1) 
(2) 
解答
(1) 
(2) 
ポイント
この公式は最も覚え間違いが発生しやすいです。
符号や係数が正しいか、何度も確認しながら解くようにしましょう。
因数分解できたら、それを逆に展開することで合っているかチェックできます。
因数分解の応用問題
基礎的な因数分解の公式は以上です。
ここから先は難しめの問題をご紹介します。
置き換えを用いる因数分解
問題
次の式を因数分解せよ。
解答
とおくと、
ここで 
と因数分解できるため、
ポイント
与えられた指揮をそのまま展開した後に因数分解するのもありですが、 x + 3 が共通していることに着目します。
ここを文字でおくことで全体をシンプルな 2 次式にでき、それを因数分解すれば OK というわけですね。
ただし自分で用意した文字で答えてはいけないので、与えられた文字を用いた式に直しておきましょう。
1 つの文字について整理する因数分解
問題
次の式を因数分解せよ。
解答
p, q のうち次数の低い q について整理すると、
ポイント
簡単には因数分解できない場合、各文字について何次式かを調べます。
そして、次数が最も小さくなった文字に着目し、式を整理してみましょう。
各係数を因数分解してから全体を見渡すと、因数分解の糸口が掴めることが多いです！
対称式・交代式の因数分解
用語
a + b や ab + bc + ca, abc のように、登場する文字のうち任意の 2 つを入れ替えても式が不変であるものを対称式といいます。
a - b や 
のように、登場する文字のうち任意の 2 つを入れ替えると式全体の符号が逆になるものを交代式といいます。
問題
次の式を因数分解せよ。
(1) 
(2) 
解答
(1)
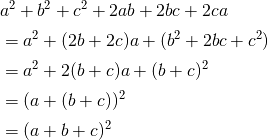
(2)
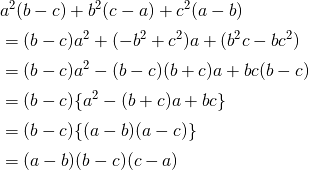
ポイント
いずれも難しい問題でしたね。
対称式の場合、特定の 1 文字に着目することで次数が下がることはありません（対称式なので）。
しかし、とりあえずある文字について整理して各係数を因数分解していけば、手数はかかりますが因数分解できます！
まとめ
数学 I で登場する様々な因数分解を紹介しました。
因数分解は、数学 I だけでなくその後の様々な分野で姿を見せる重要な操作です。
「基礎的な因数分解の問題を総ざらい」のところで紹介した問題は、全て自力で解けるようにしておきましょう！