スタクラ情報局

絶対値を含む不等式

高校数学 I で１次不等式を学習しますが、そこで手強いのが絶対値記号のある不等式。

真っ直ぐに計算していくことができず場合分けが必要なので、苦手意識のある高校生は多いことでしょう。

そこで今回は、絶対値記号のある不等式の攻略方法を見ていきます。

この記事で苦手を克服しちゃいましょう！

絶対値とは

そもそも絶対値とはどういうものか。

ここではそれを学習します。

"原点からの距離"

まずは簡単な例題から。

例題

以下の数の絶対値を求めよ。

(1) 5
(2) -3
(3) 0

絶対値は、簡単にいうと「数直線上での原点 (0)からの距離」のことです。

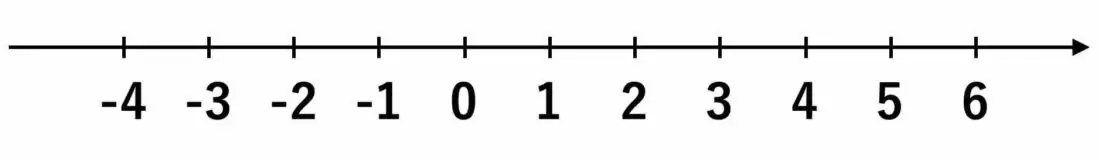
そもそも数直線とは、上図のように数を一直線に並べたものでした。

※イメージしやすくするために整数のみ表示していますが、小数や分数も数直線上にあります。

ではこの数直線に、例題の 3 つの数を図示してみましょう。

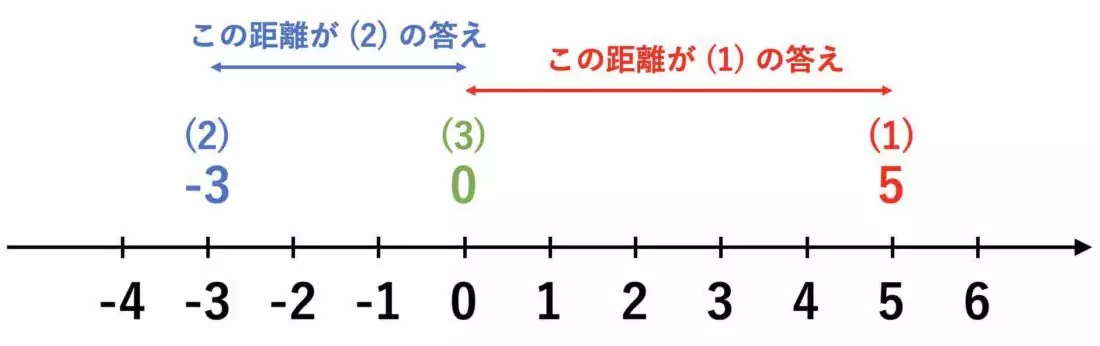
絶対値は、数直線上での原点からの距離、つまり両矢印の長さに他なりません。

したがって (1) の答えは 5 であり、(2) の答えは 3 です。

0 というのは数直線の原点そのものなので、(3) の答えは 0 となります。]

同様に、例えば の絶対値は であり、 の絶対値は  です。

絶対値記号

絶対値は、その数の両脇に縦棒（｜）を書くことで表します。

例えば 5 の絶対値は  と書き、 となります。

同様に ,  ,  ,   となります。

絶対値の定義を文字で書くと

これまでは決まった値の絶対値を考えていました。

では、ある実数 x の絶対値 |x| を計算するとどうなるでしょうか？

これまでの例を考えてみましょう。

,  といった式から、絶対値記号の中身が正であれば絶対値の値は "そのまま" とわかります。

一方で ,  といった指揮を見ると、絶対値記号の中身が負のときの絶対値の値は "逆符号" です。

※ 0 の絶対値は 0 であり、符号をそのままにしても逆にしても同じことですね。

というわけで、一般の数 |x| の絶対値を計算するときは x 自体の符号によって話が変わってきます。

絶対値 |x| の定義は次の通りです：

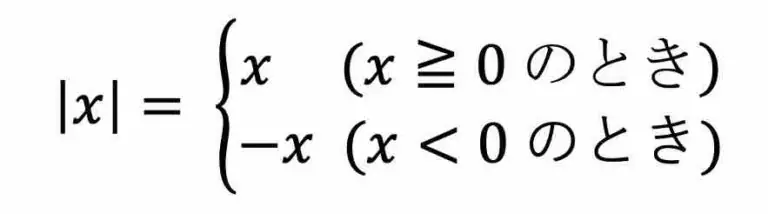
この定義が出発点となるので、ここで頭に入れておきましょう。

これを蔑ろにしていると、絶対値つきの不等式が理解できなくなります。

絶対値つきの不等式の解き方

以上の内容を踏まえ、絶対値つきの不等式の解き方を見ていきましょう。

|x| だけのもの

まずは不等式に |x| しか登場しないものです。

問題

次の不等式を解け。

|x| < 3

解答

i) x ≧ 0 のとき
|x| = x であるため x < 3
x ≧ 0 に注意して 0 ≦ x < 3

ii) x < 0 のとき
|x| = -x であるため -x < 3 つまり x > -3
x < 0 に注意して -3 < x < 0

i), ii) を合わせて -3 < x < 3

ポイント

絶対値記号の定義を思い出しましょう。

今回の場合 x の正負によって場合分けが必要です。

各々の場合分けで不等式を解き、それらを合わせて不等式の答えを出します。

絶対値の意味を理解している場合は、いきなり |x| < 3 から -3 < x < 3 と計算できます。

絶対値というのは数直線上での原点からの距離であったためです。

なお、解答の太字部分に注意してください。

| x - a | タイプ

次は少々レベルアップして、絶対値記号の中に定数が加わります。

問題

次の不等式を解け。

|x - 1| > 2

解答

i) x - 1 ≧ 0 つまり x ≧ 1 のとき
|x - 1| = x - 1 より x - 1 > 2 つまり x > 3
x ≧ 1 に注意して x > 3

ii) x - 1 < 0 つまり x < 1 のとき
|x - 1| = -(x - 1) = 1 - x より 1 - x > 2 つまり x < -1
x < 1 に注意して x < -1

i), ii) より x < -1, x > 3

ポイント

絶対値記号の中身が複雑になりましたが、やることは一緒。

絶対値記号の中身の正負で場合分けをするだけです。（赤字部）

ちなみに、今回の解も数直線で表示すると納得しやすいです：

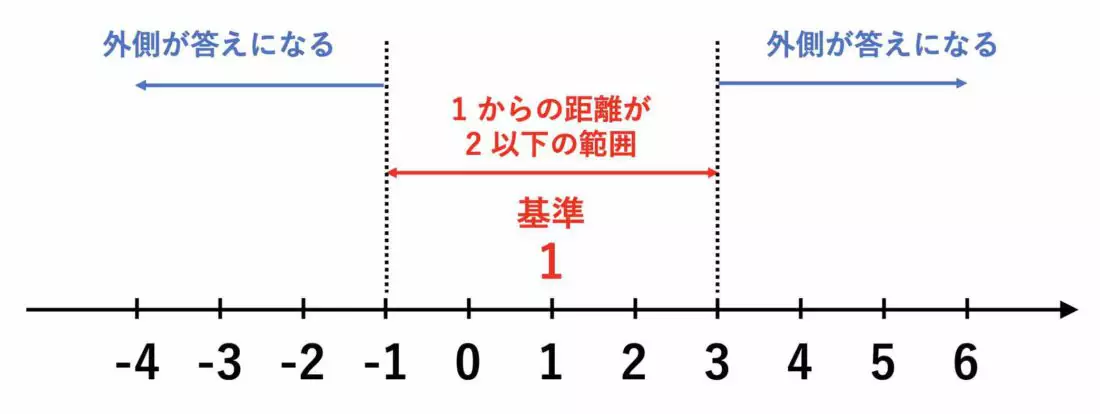
|x - 1| > 2 は、数直線で "1" からの距離が 2 より大きいことを意味します。

"1" からの距離が 2 以下であるのは上図の赤矢印ですね。

したがって、その外側（青矢印、大きい方にも小さい方にも存在）が解となるのです。

絶対値以外にも x があるタイプ

問題

次の不等式を解け。

|4 - x| > x

解答

i) 4 - x ≧ 0 つまり x ≦ 4 のとき

|4 - x| = 4 - x より 4 - x > x, よって x < 2

x  ≦ 4 に注意して x < 2

ii) 4 - x < 0 つまり x > 4 のとき

|4 - x| = x - 4 より x - 4 > x つまり -4 > 0

これを満たす x は存在しない。

i), ii) より x < 2

ポイント

前の問題と異なり右辺にも x がありますが、場合分けの仕方自体は変わりません。

絶対値記号の中身が正（ 0 以上）の場合と負の場合に分けて、それぞれの場合で不等式を解けば OK です。

複数の絶対値記号があるタイプ

では最後に、複数の絶対値記号が登場する不等式を攻略します。

問題

次の不等式を解け。

|7 - x| > |2x + 5|

解答

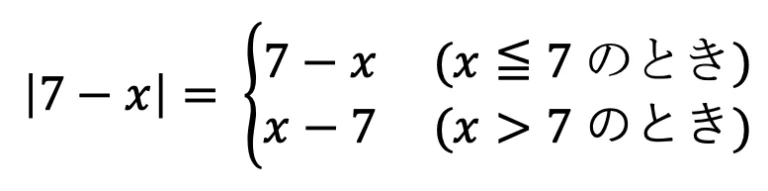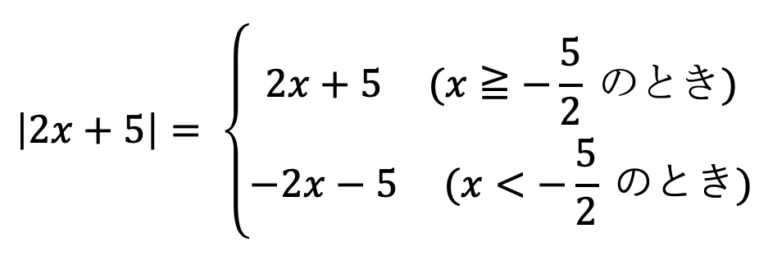,    であることを用いると以下のようになる。

i)  のとき
7 - x > -2x - 5 より x > -12
に注意して

ii)  のとき
7 - x > 2x + 5 より
に注意して

iii) x > 7 のとき
x - 7 > 2x + 5 より x < -12
これと x > 7 を同時に満たす x は存在しない。

i), ii), iii) より

ポイント

難しい問題でした。

絶対値記号が複数あるので、その各々について場合分けが必要となります。

これまで 2 つの場合分けであったのに今回は 3 つであるのはそのためです。

イメージ的には次の通りです。

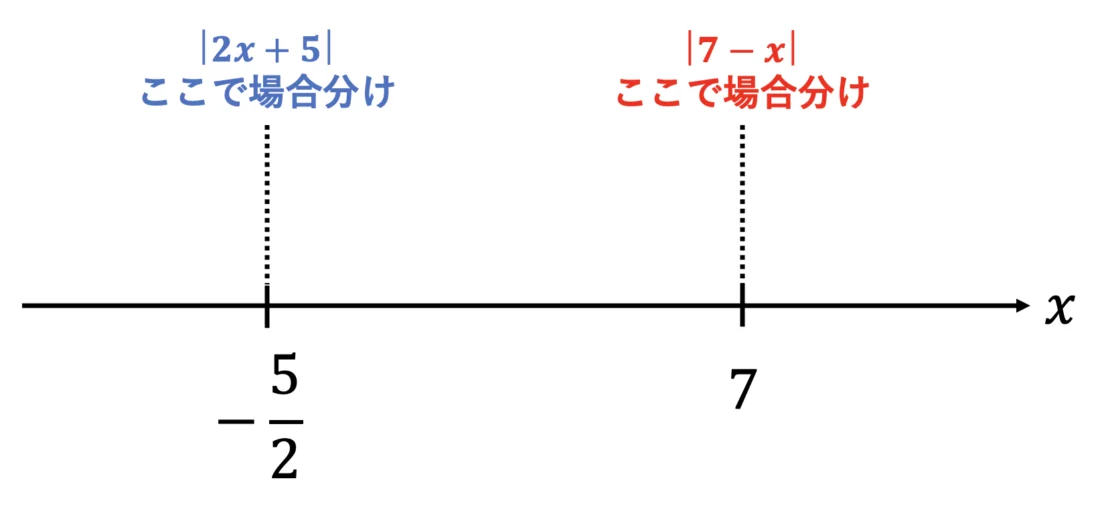
確かに、数直線が 3 つに分かれていますね。

まとめ

今回は、絶対値記号を含む不等式の解法を紹介しました。

まずは何より、

• 絶対値の定義

• |x| の場合分け

をマスターするのが先決です。

複雑な問題でも、上記 2 点をよく理解していれば解答することができます。

よく読み返して、この記事の問題は全て解けるようにしておきましょう！